Experience the timeless beauty of solution: chapter 3 direct algorithms of decompositions of matrices by with our curated gallery of vast arrays of images. showcasing the classic style of photography, images, and pictures. perfect for retro design and marketing. Each solution: chapter 3 direct algorithms of decompositions of matrices by image is carefully selected for superior visual impact and professional quality. Suitable for various applications including web design, social media, personal projects, and digital content creation All solution: chapter 3 direct algorithms of decompositions of matrices by images are available in high resolution with professional-grade quality, optimized for both digital and print applications, and include comprehensive metadata for easy organization and usage. Explore the versatility of our solution: chapter 3 direct algorithms of decompositions of matrices by collection for various creative and professional projects. Whether for commercial projects or personal use, our solution: chapter 3 direct algorithms of decompositions of matrices by collection delivers consistent excellence. Multiple resolution options ensure optimal performance across different platforms and applications. Instant download capabilities enable immediate access to chosen solution: chapter 3 direct algorithms of decompositions of matrices by images. Our solution: chapter 3 direct algorithms of decompositions of matrices by database continuously expands with fresh, relevant content from skilled photographers.













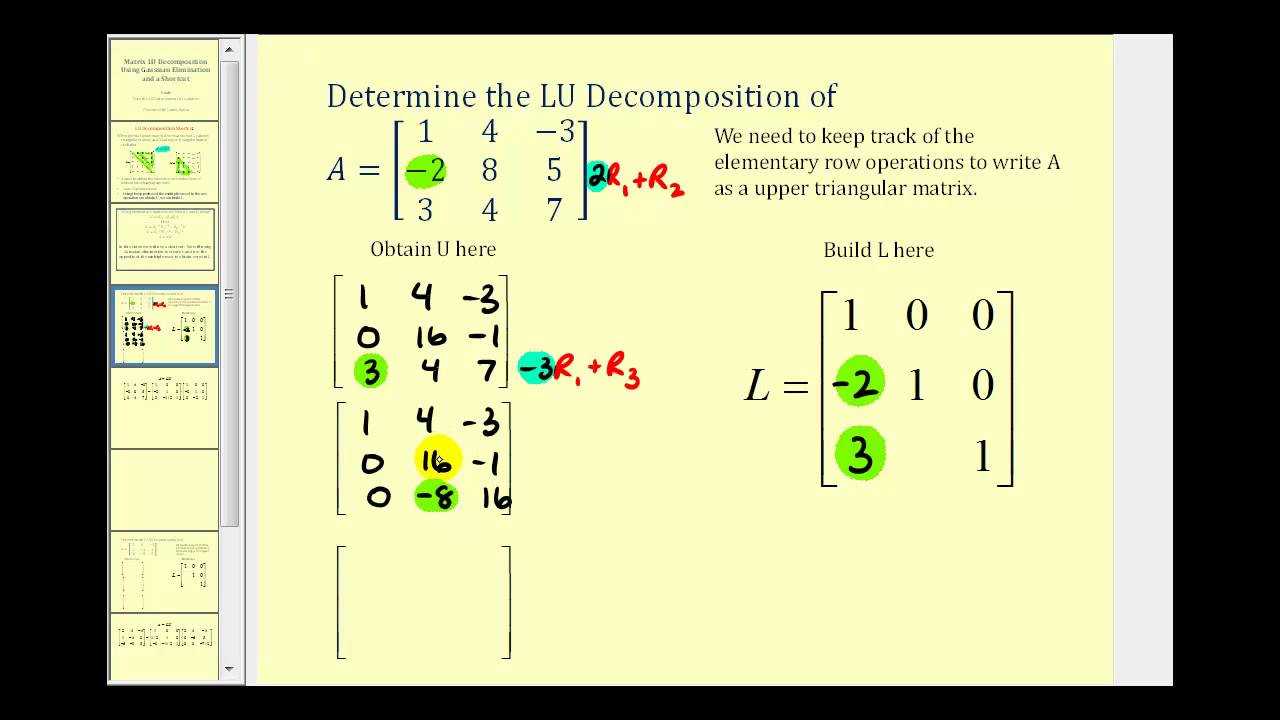
![SOLVED: Consider the 3x3 matrix A = [4, -2, 4; -2, 5, -4; 4, -4, 15] (a ...](https://cdn.numerade.com/ask_images/8cfcc6933f504029aa9593dd7d38a1d3.jpg)







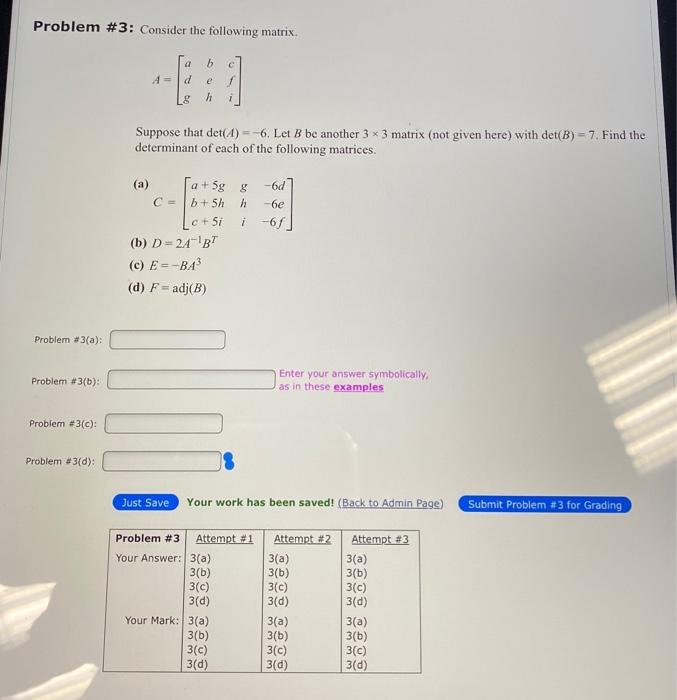



























.jpg)
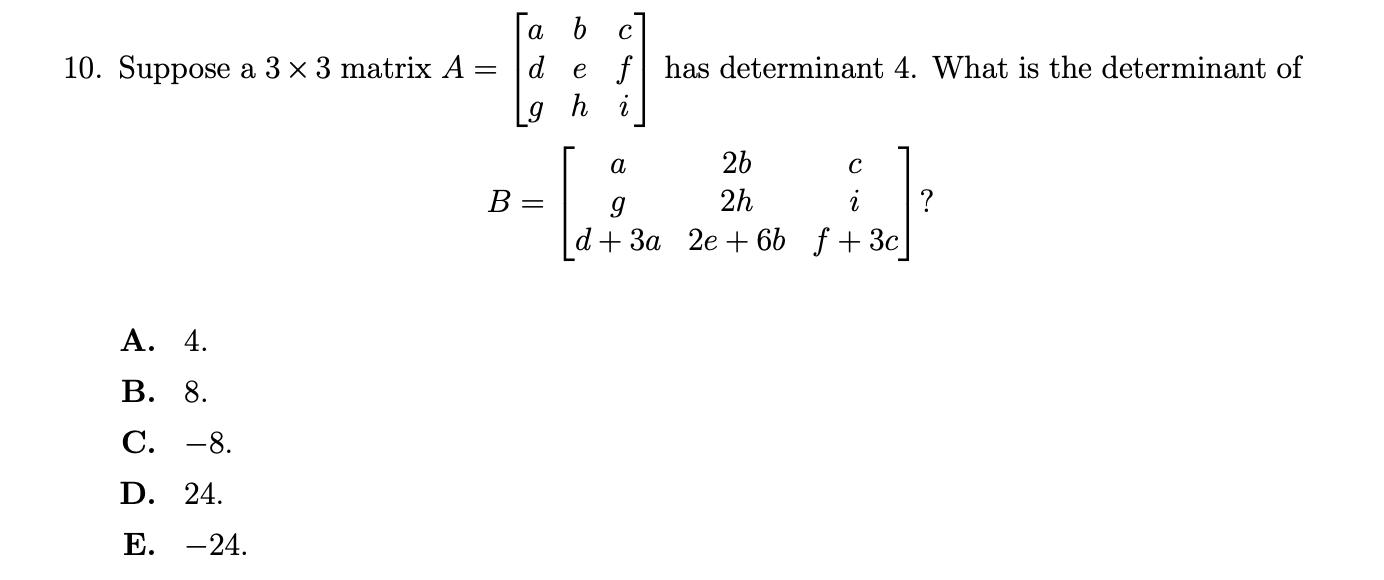














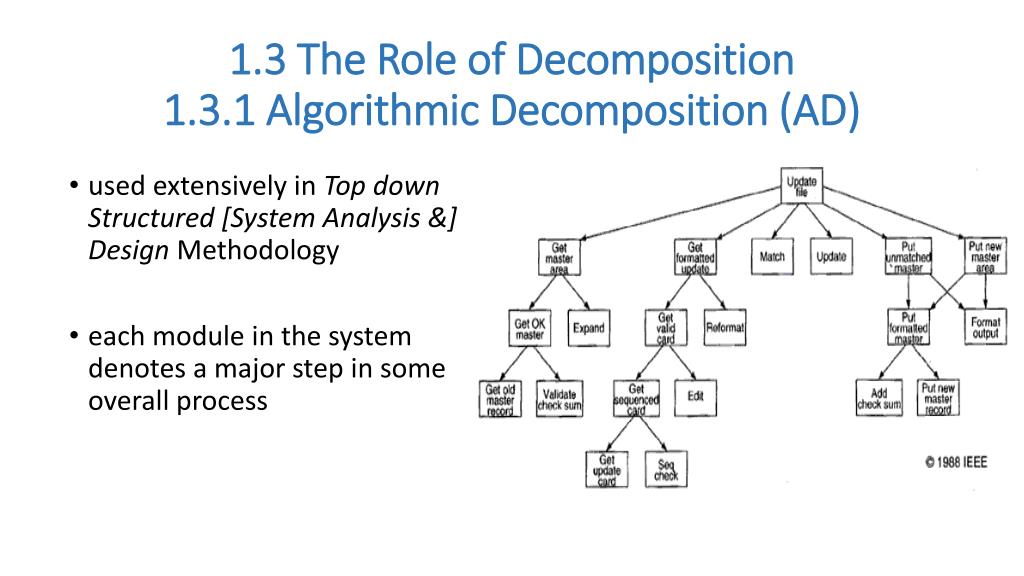



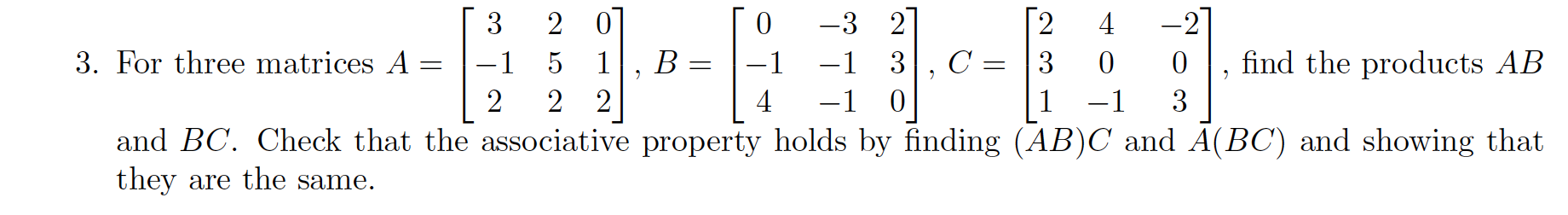
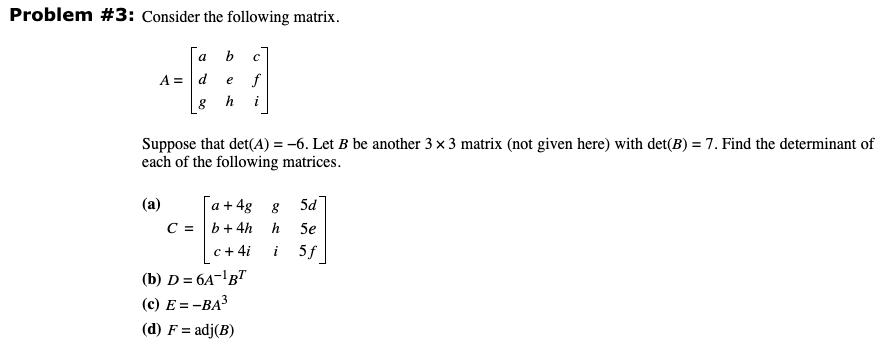
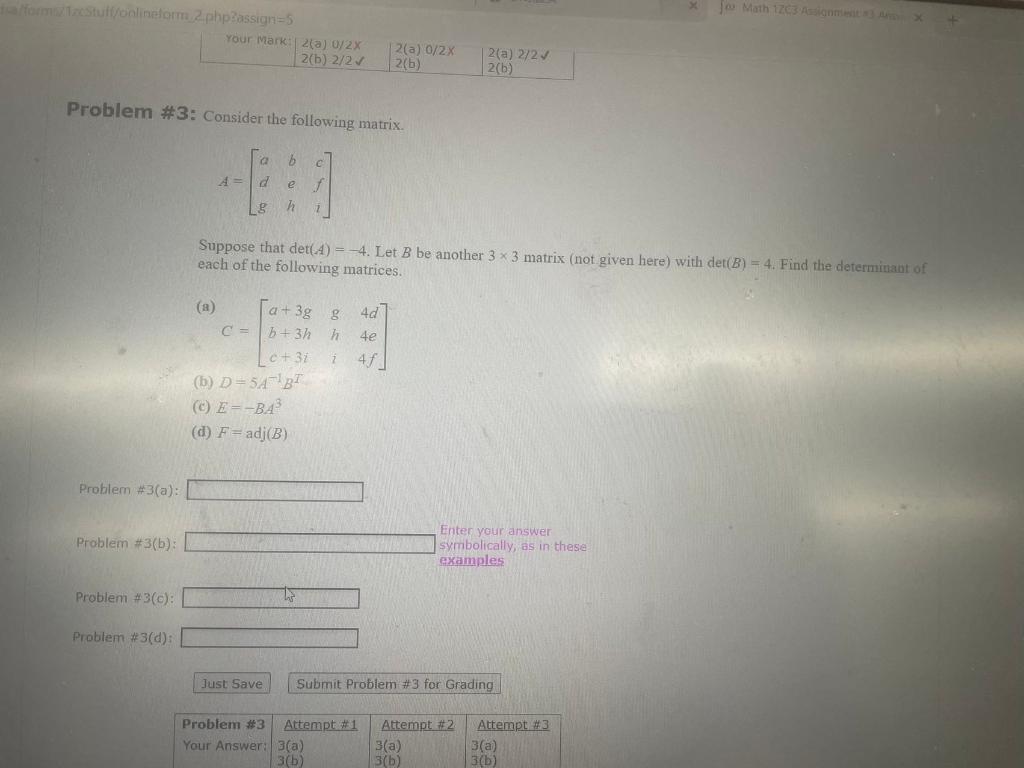




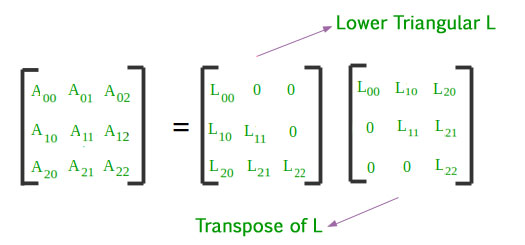
![Solved PROBLEM 1. Let --[ A = I 2 4 -2 1 3 ] -1 3 5 5 [2]a) | Chegg.com](https://d2vlcm61l7u1fs.cloudfront.net/media/941/9410512c-eee6-4ce7-8481-67d766e62976/phpSGvMg8.png)
![Solved PROBLEM 1 Consider the following matrix A: 11 1 1] A= | Chegg.com](https://media.cheggcdn.com/media/e67/e67b097c-e296-4ee0-81b9-0efcf678da00/phpqwBTUI)


![Solved Consider the matrix A = [8 3 2 5 7 3 1 4 9] | Chegg.com](https://d2vlcm61l7u1fs.cloudfront.net/media/96c/96c775aa-34f4-4f23-aa97-c6160d811468/image)





![Solved Given the LU decomposition of a 3 x 3 matrix [A] is | Chegg.com](https://media.cheggcdn.com/study/72d/72dd9bd4-5b8d-4893-9f08-97bf454db641/image.png)