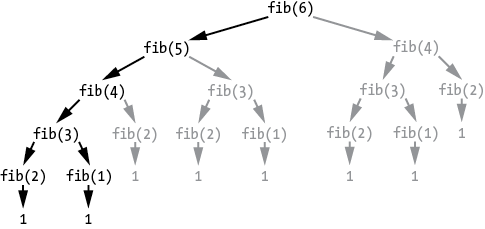
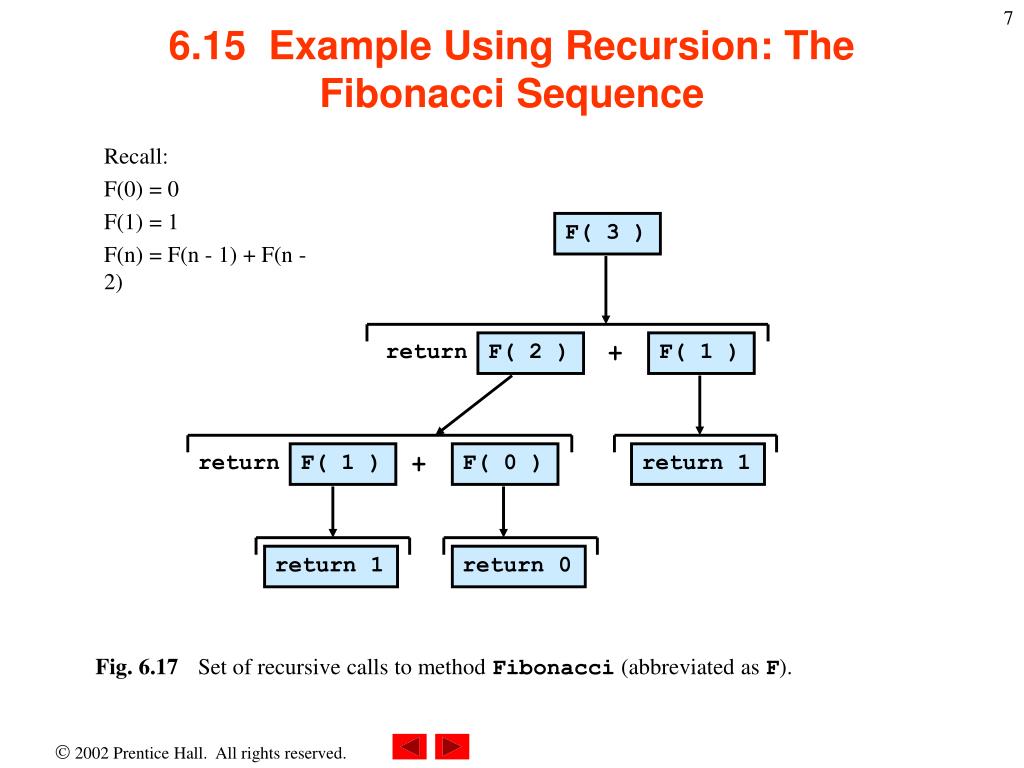
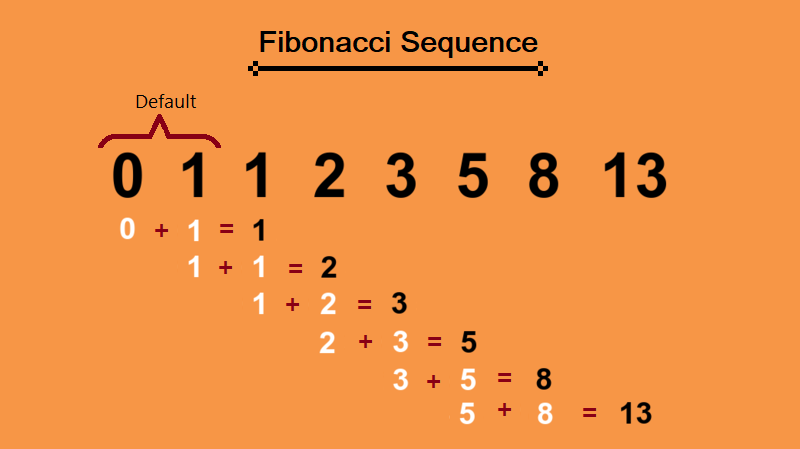
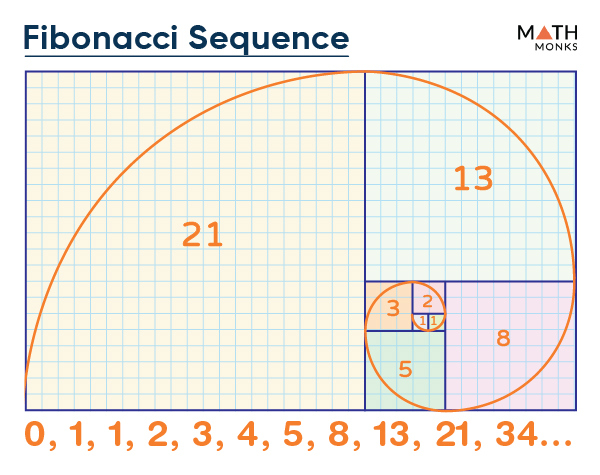
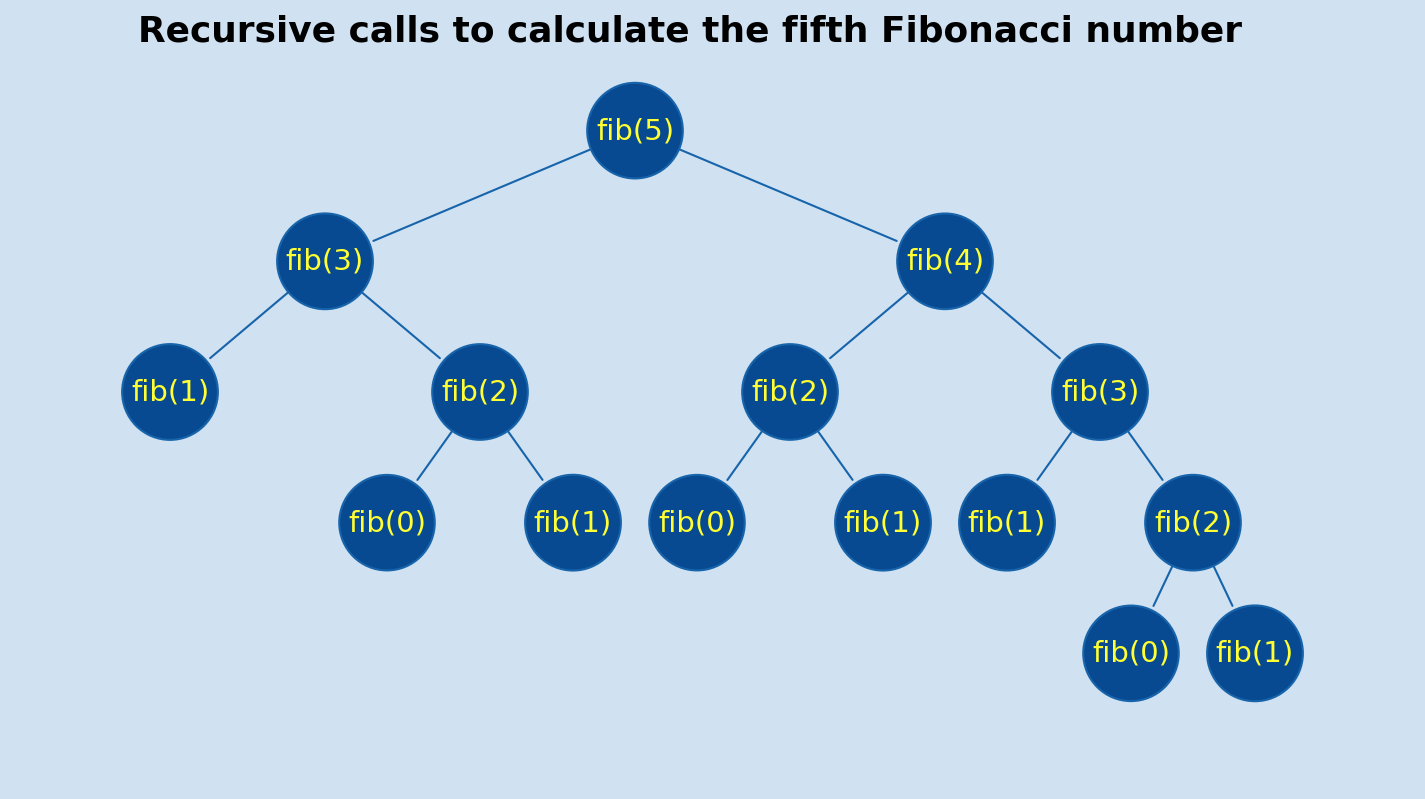
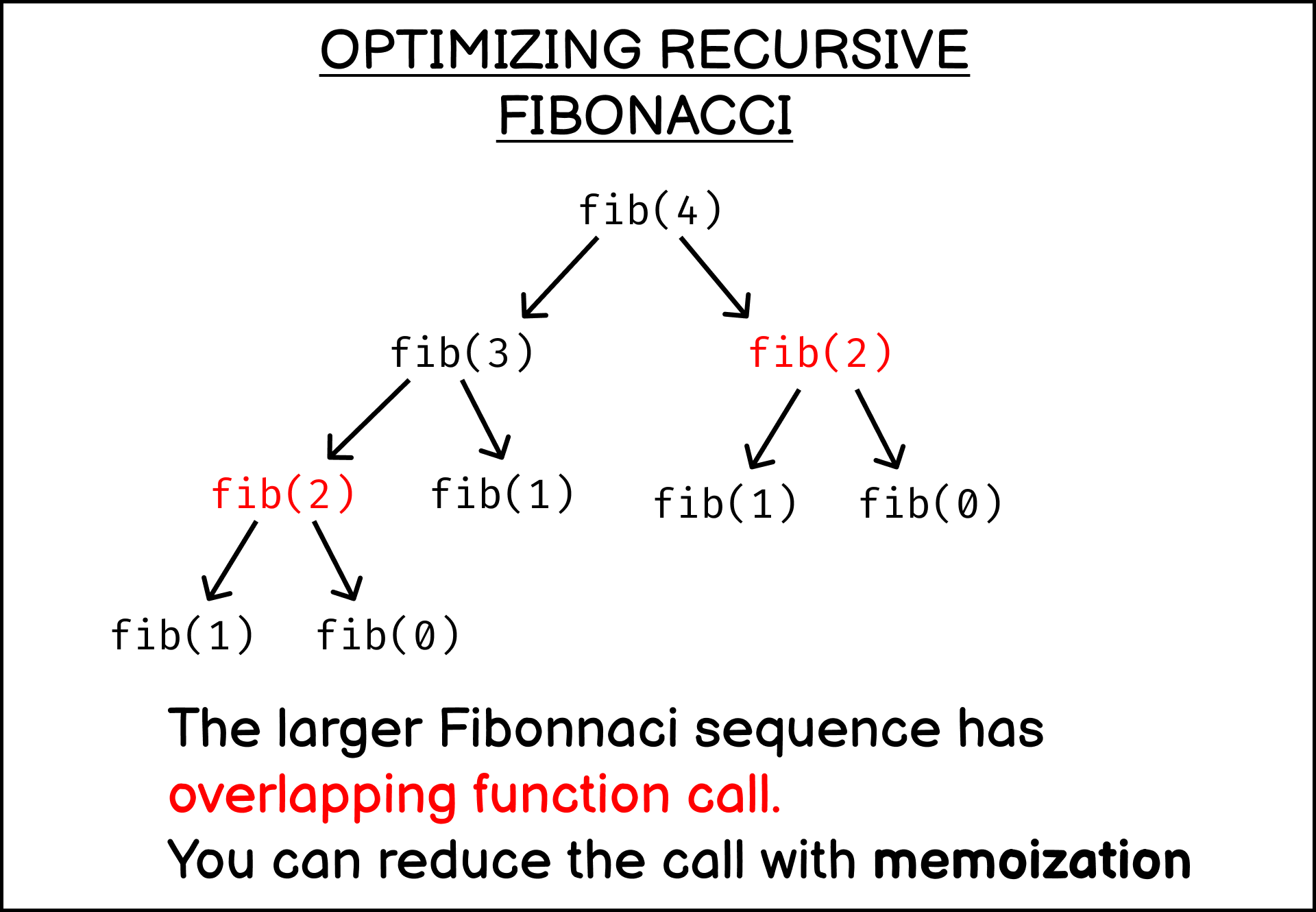
Recursive Algorithm For Fibonacci Series
Capture truth through numerous documentary-style Recursive Algorithm For Fibonacci Series photographs. honestly portraying photography, images, and pictures. perfect for journalism and news reporting. Each Recursive Algorithm For Fibonacci Series image is carefully selected for superior visual impact and professional quality. Suitable for various applications including web design, social media, personal projects, and digital content creation All Recursive Algorithm For Fibonacci Series images are available in high resolution with professional-grade quality, optimized for both digital and print applications, and include comprehensive metadata for easy organization and usage. Discover the perfect Recursive Algorithm For Fibonacci Series images to enhance your visual communication needs. Each image in our Recursive Algorithm For Fibonacci Series gallery undergoes rigorous quality assessment before inclusion. Our Recursive Algorithm For Fibonacci Series database continuously expands with fresh, relevant content from skilled photographers. The Recursive Algorithm For Fibonacci Series collection represents years of careful curation and professional standards. Reliable customer support ensures smooth experience throughout the Recursive Algorithm For Fibonacci Series selection process. Time-saving browsing features help users locate ideal Recursive Algorithm For Fibonacci Series images quickly. Cost-effective licensing makes professional Recursive Algorithm For Fibonacci Series photography accessible to all budgets. Professional licensing options accommodate both commercial and educational usage requirements.




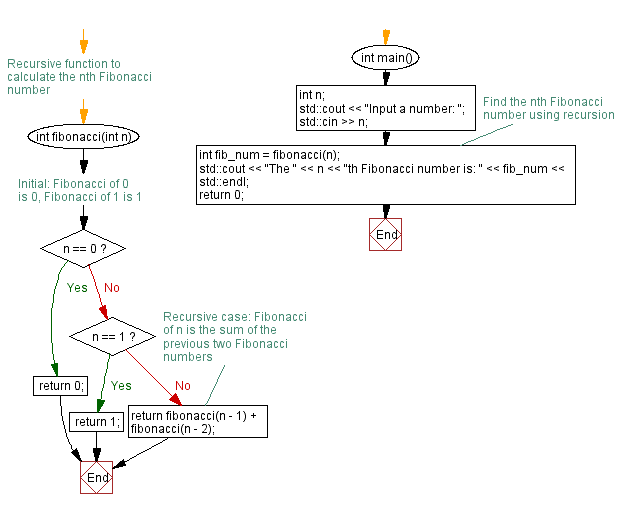





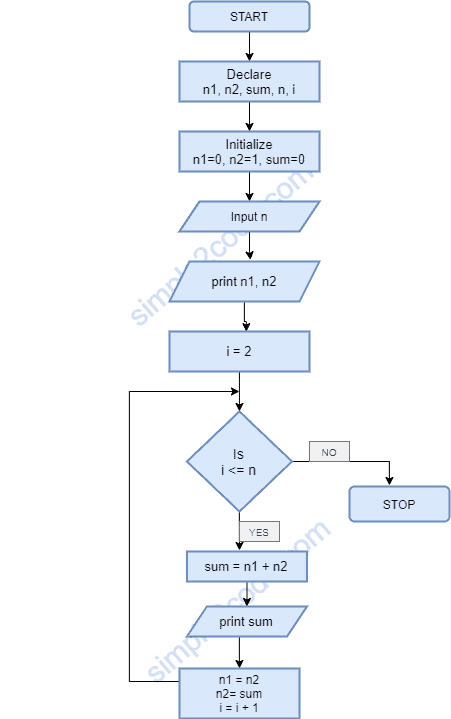

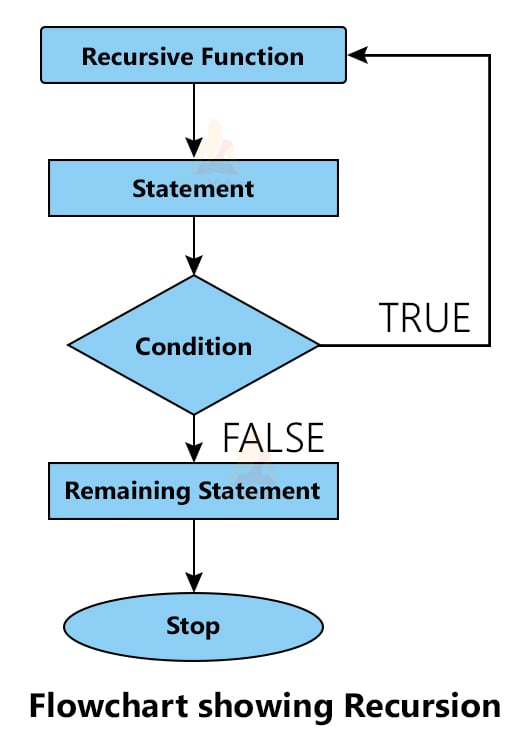




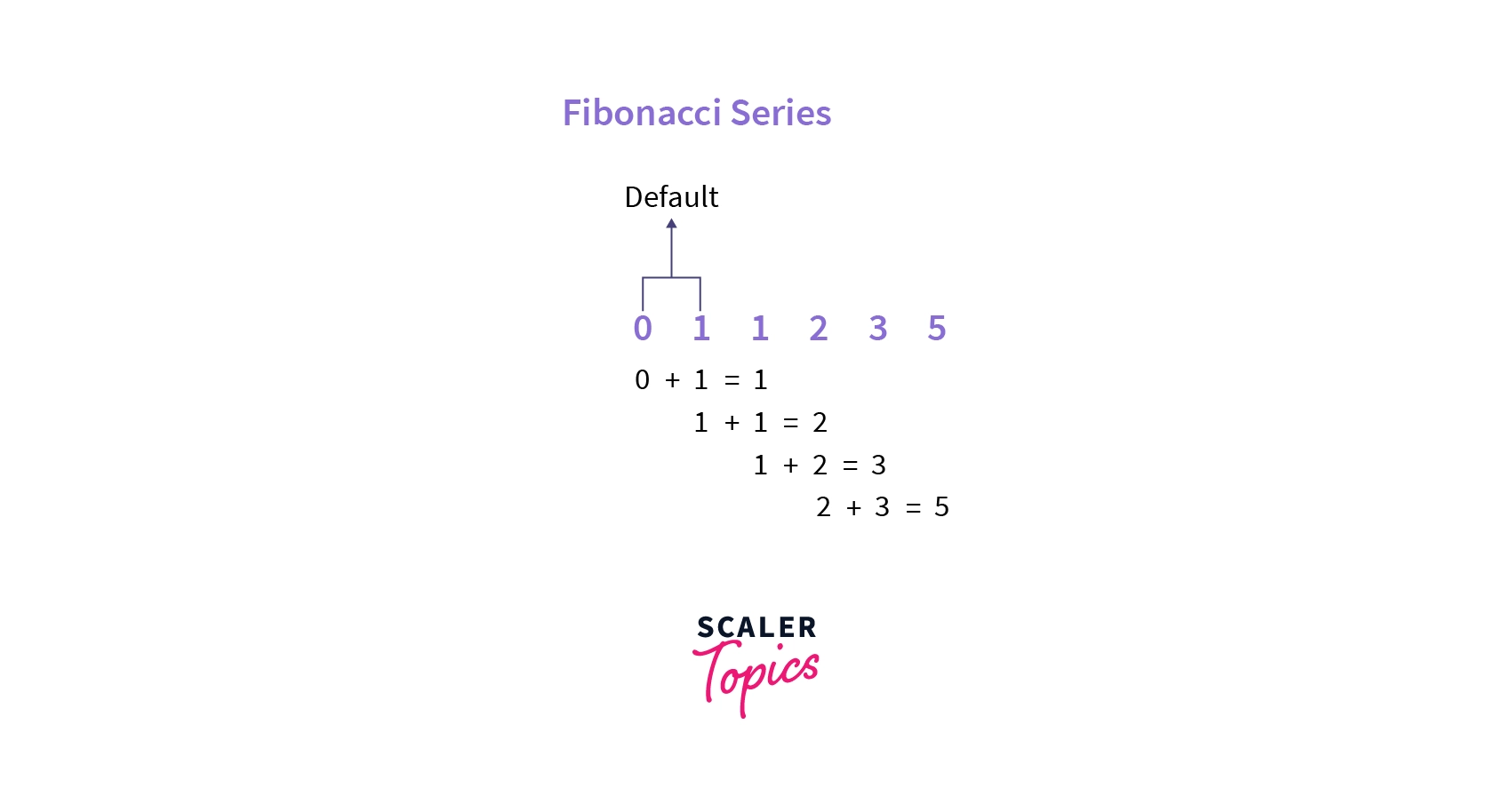



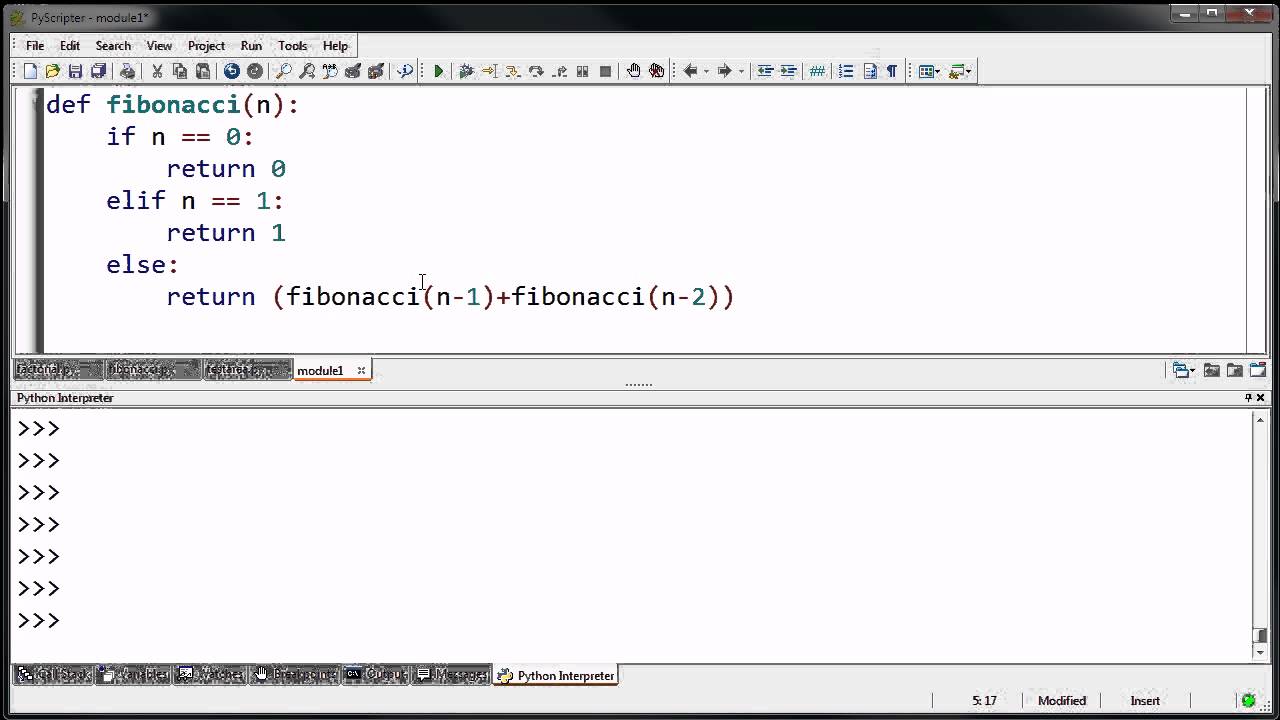
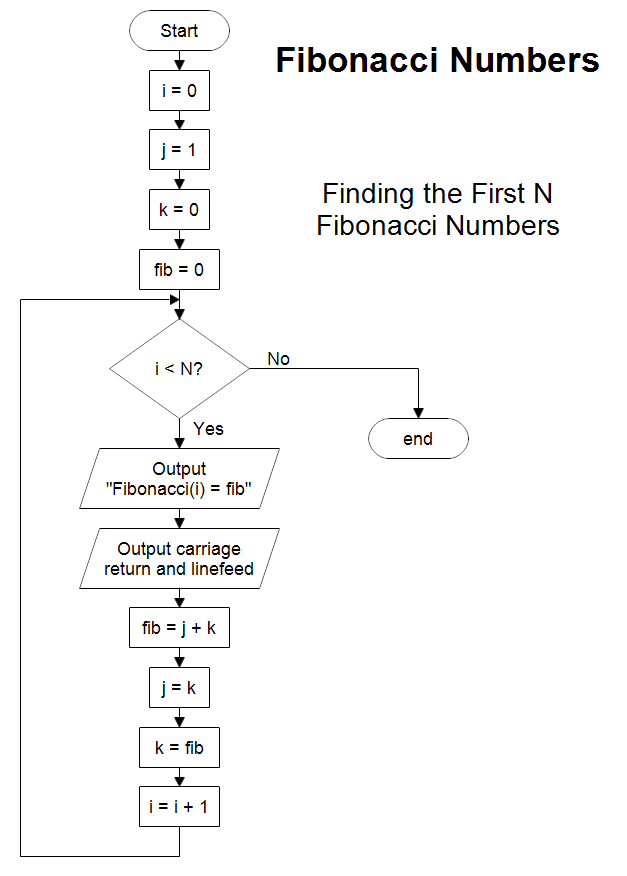






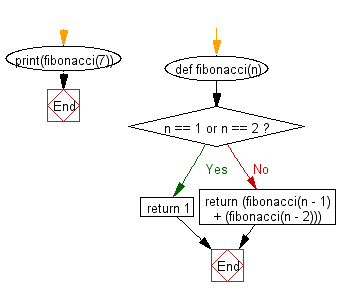
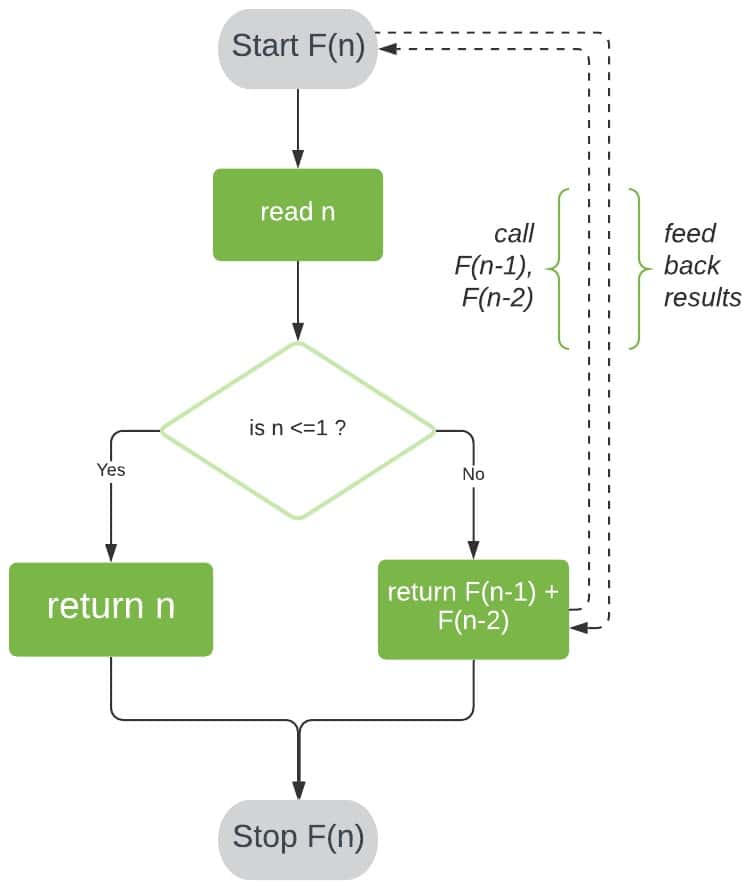
![[Computer Science] Draw a flowchart to generate the Fibonacci Series](https://cdn.teachoo.com/large/907e6f4b-fb5a-4297-aea4-b41a81c4f988/flowchart-to-generate-the-fibonacci-series---teachoo.jpg)
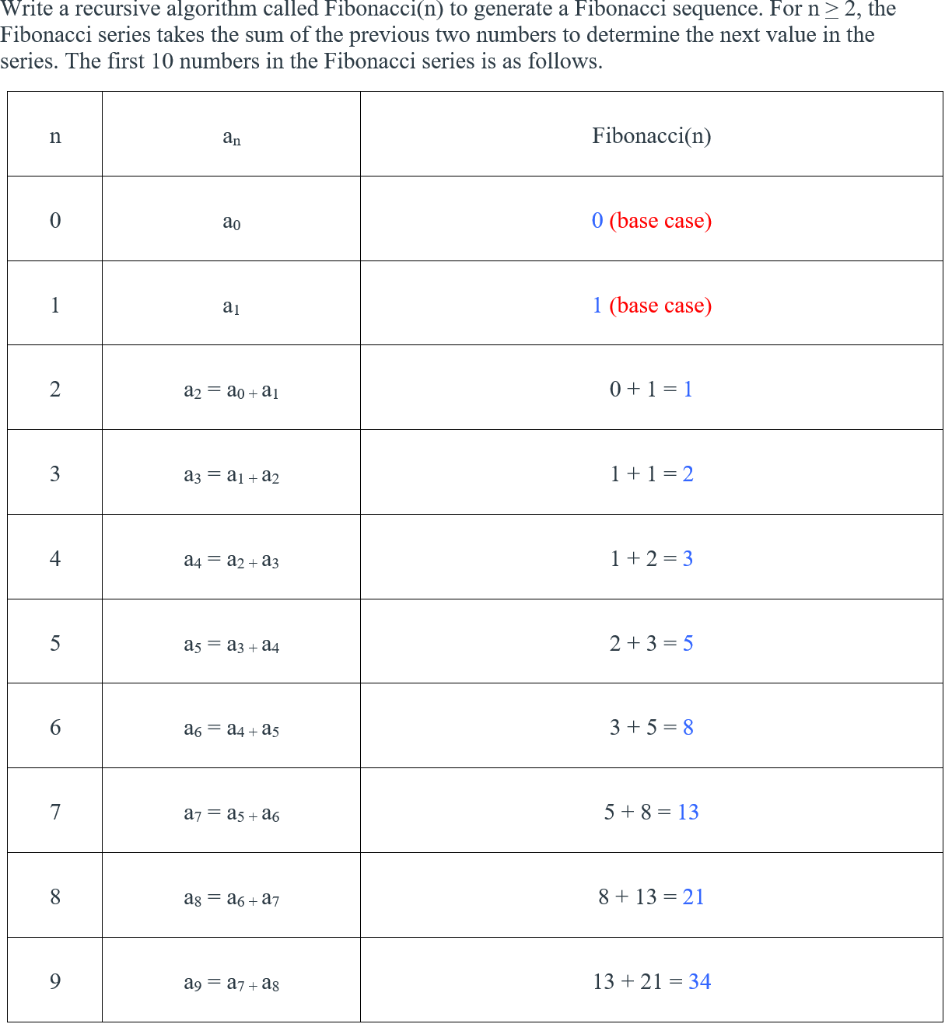

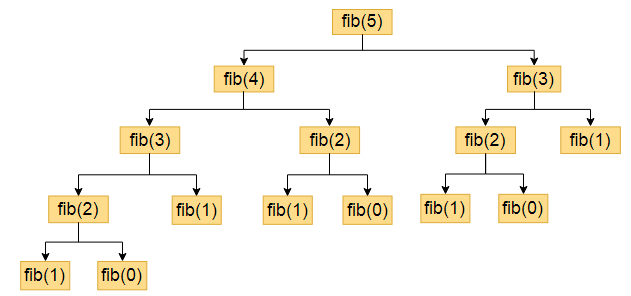

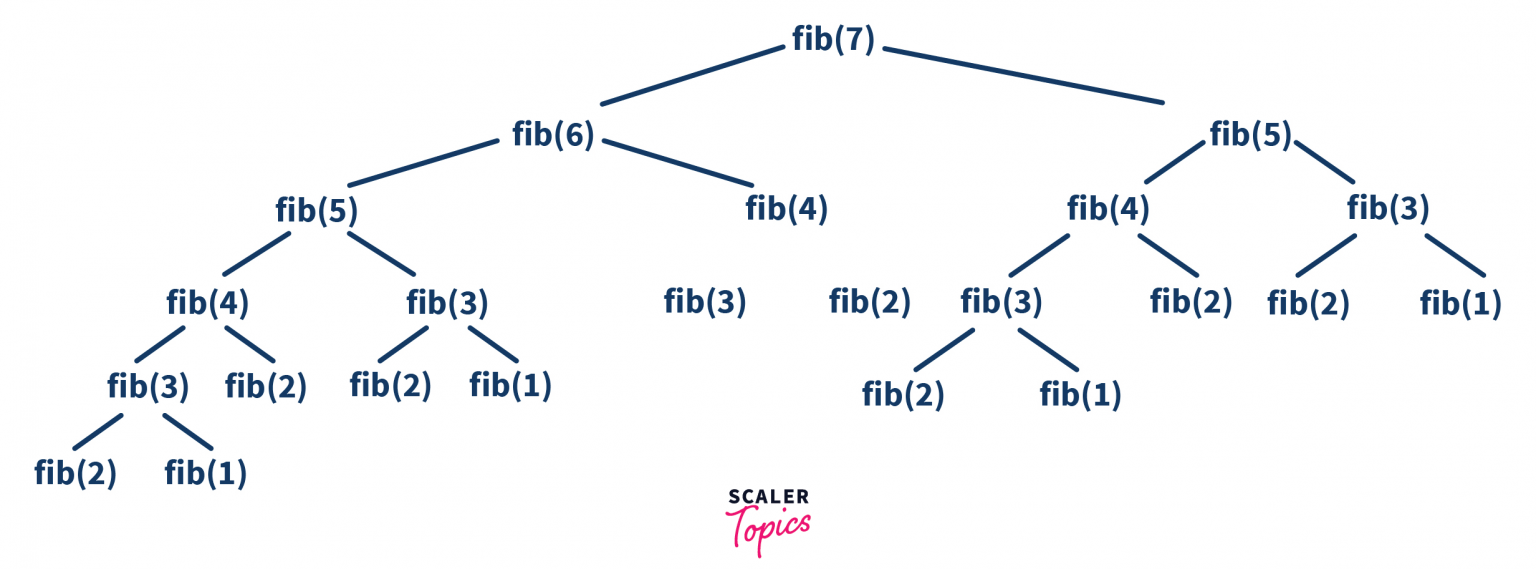

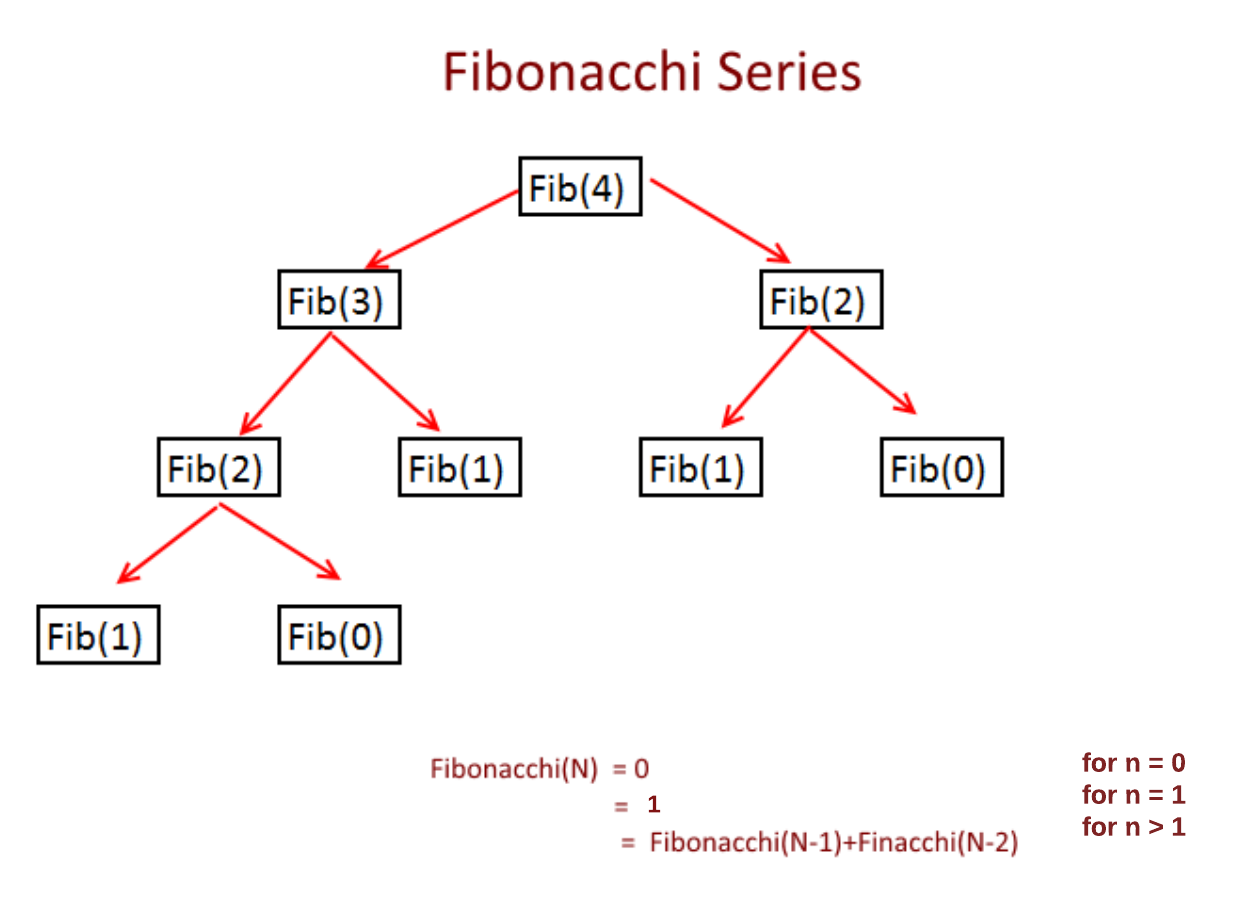

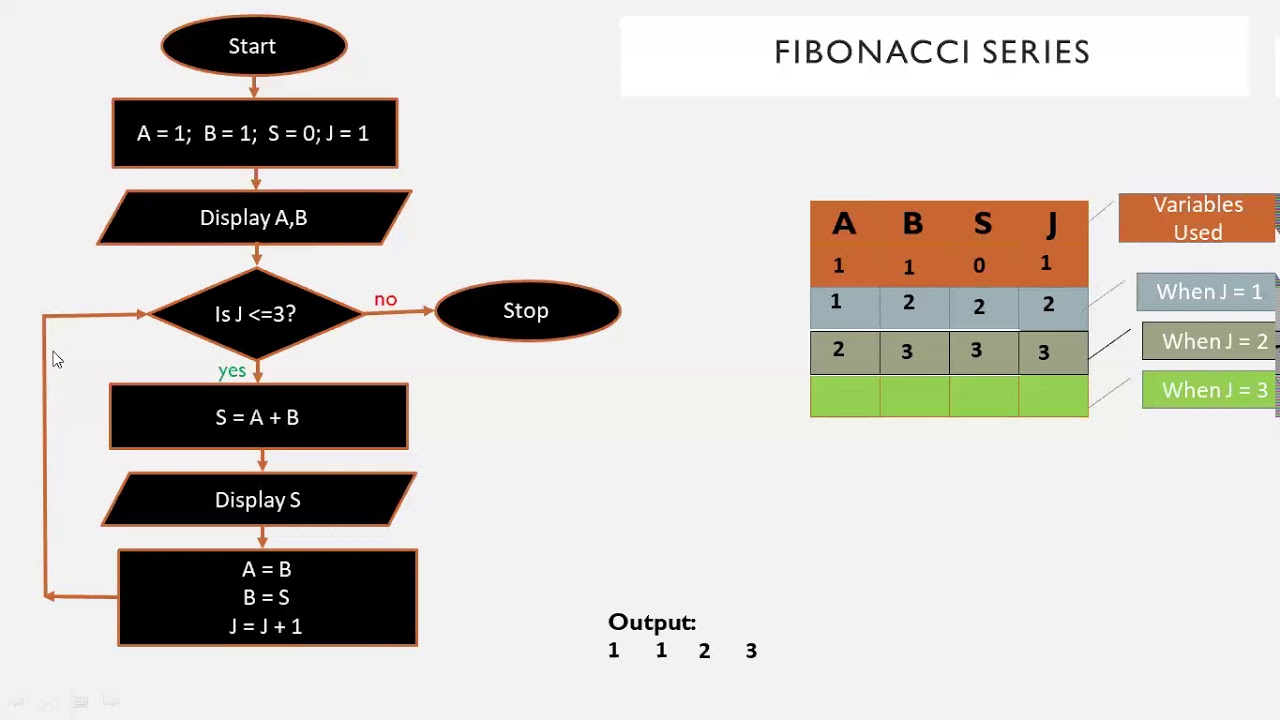
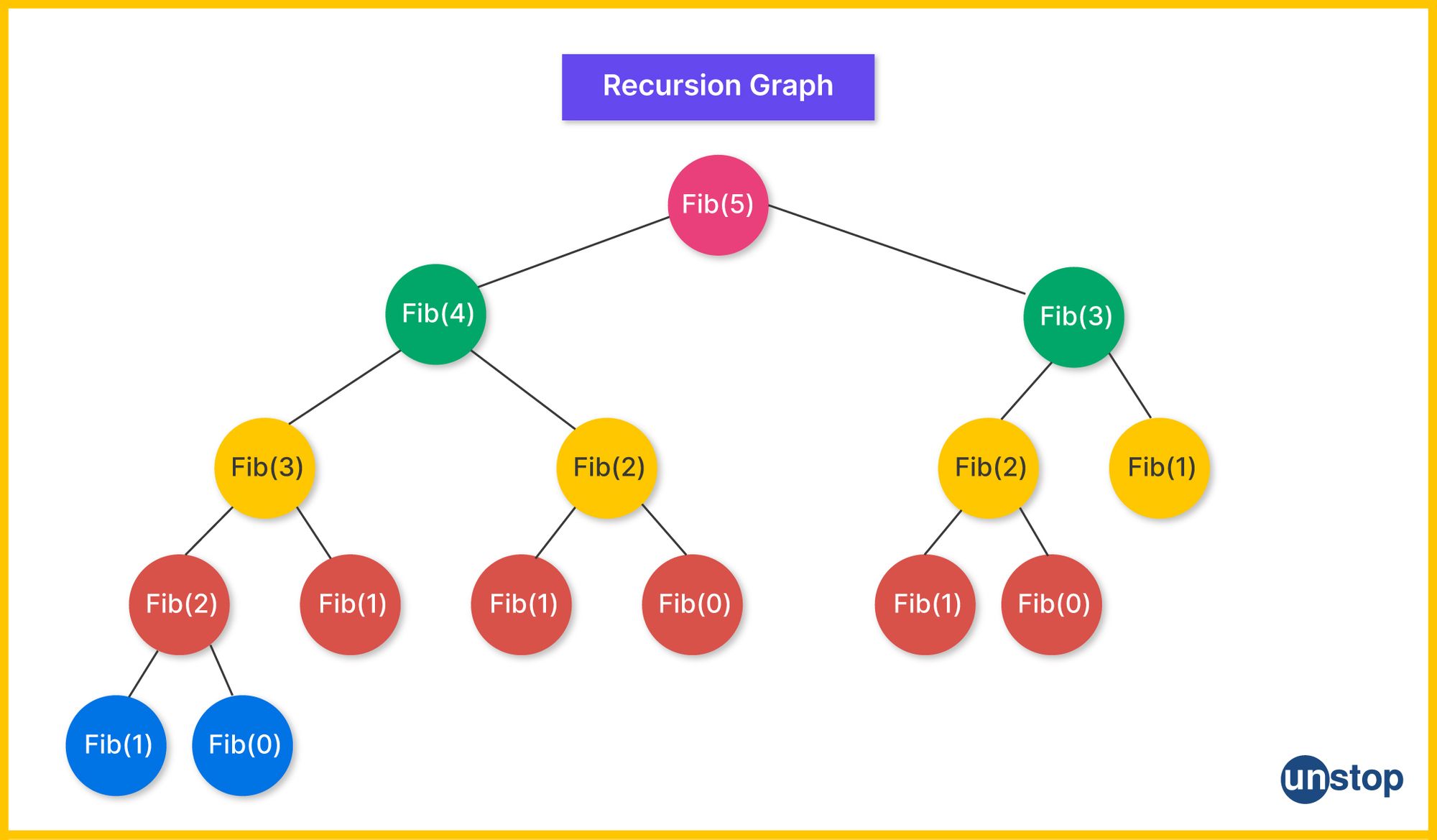



.jpg)



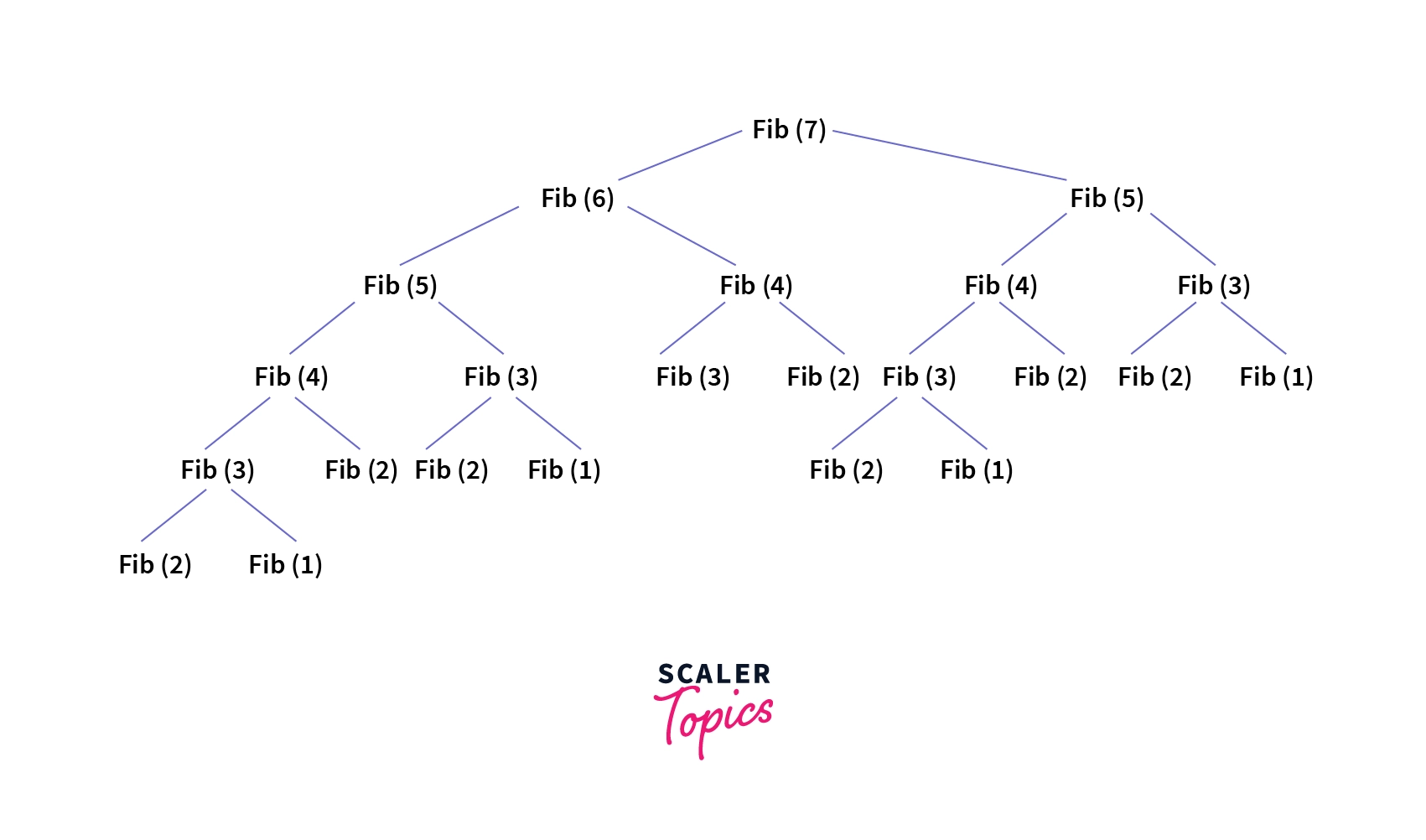
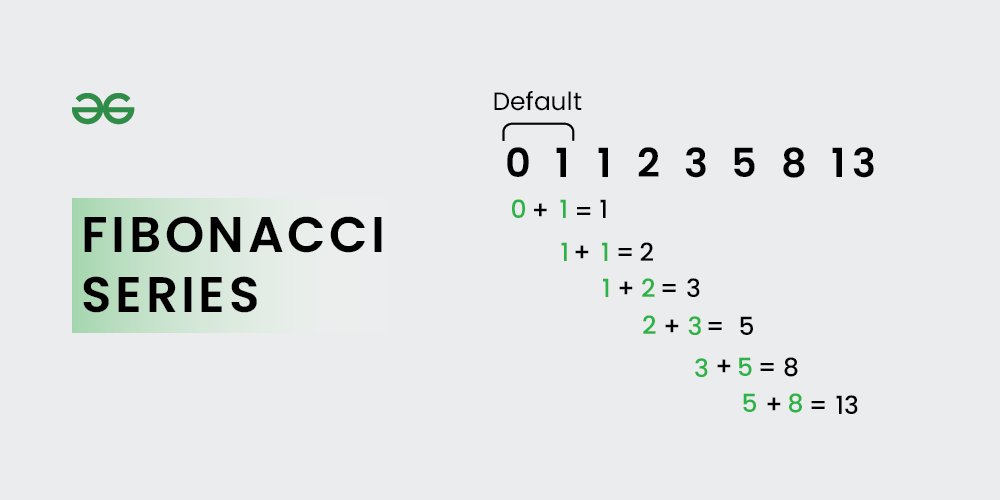
![Free Fibonacci Series in Python course with Certificate [2025]](https://dtmvamahs40ux.cloudfront.net/gl-academy/course/course-1136-imresizer.com.jpg)

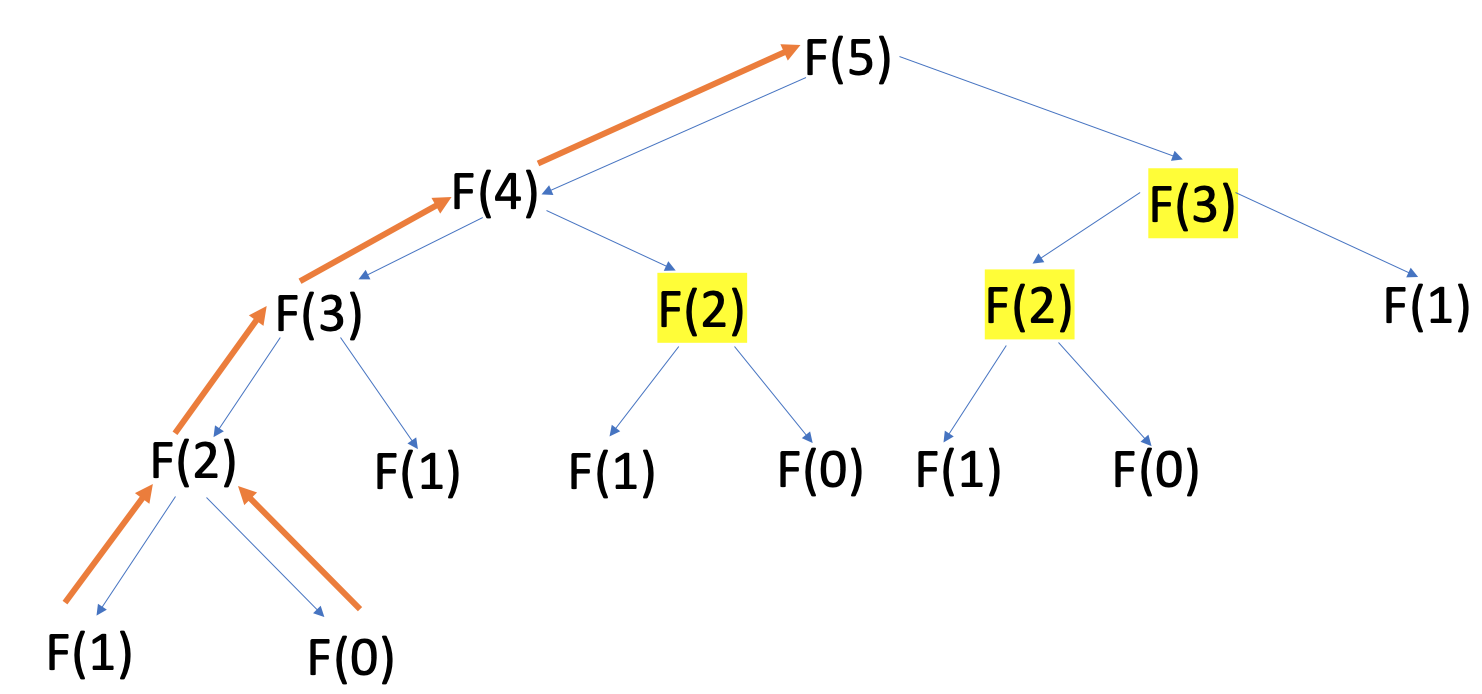

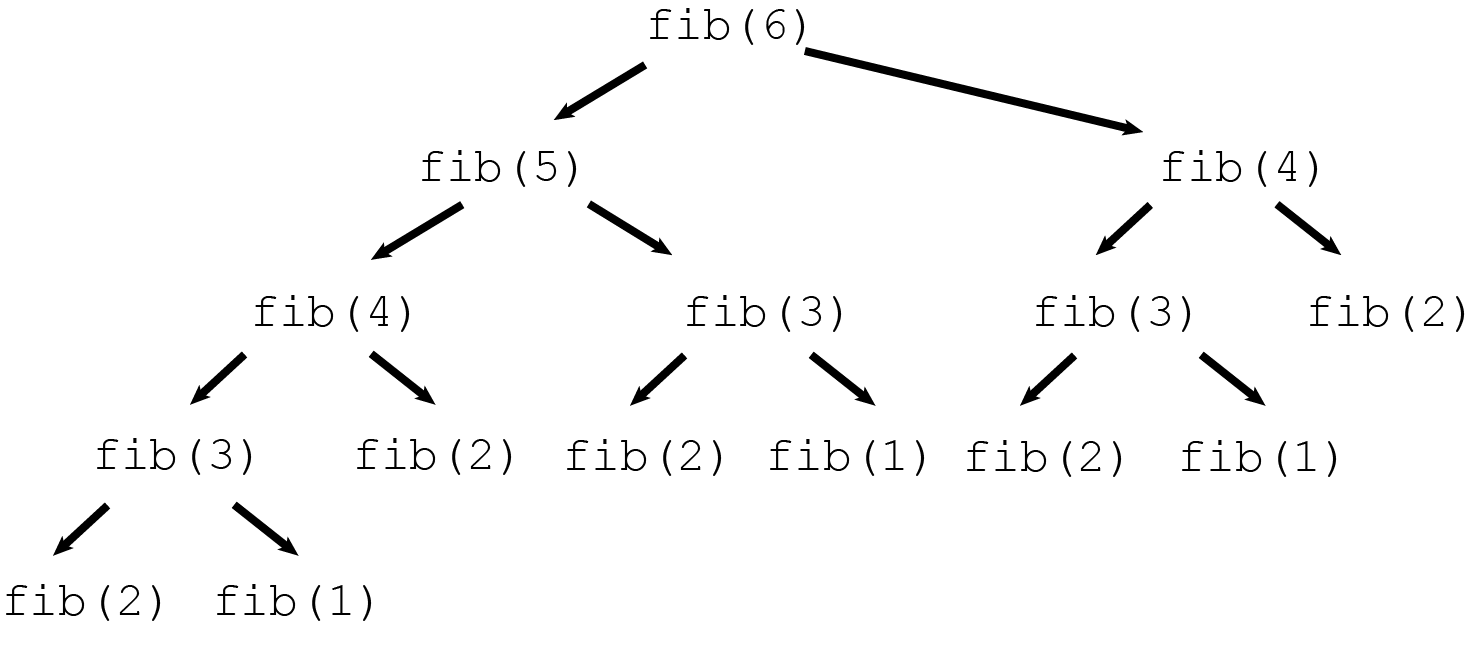
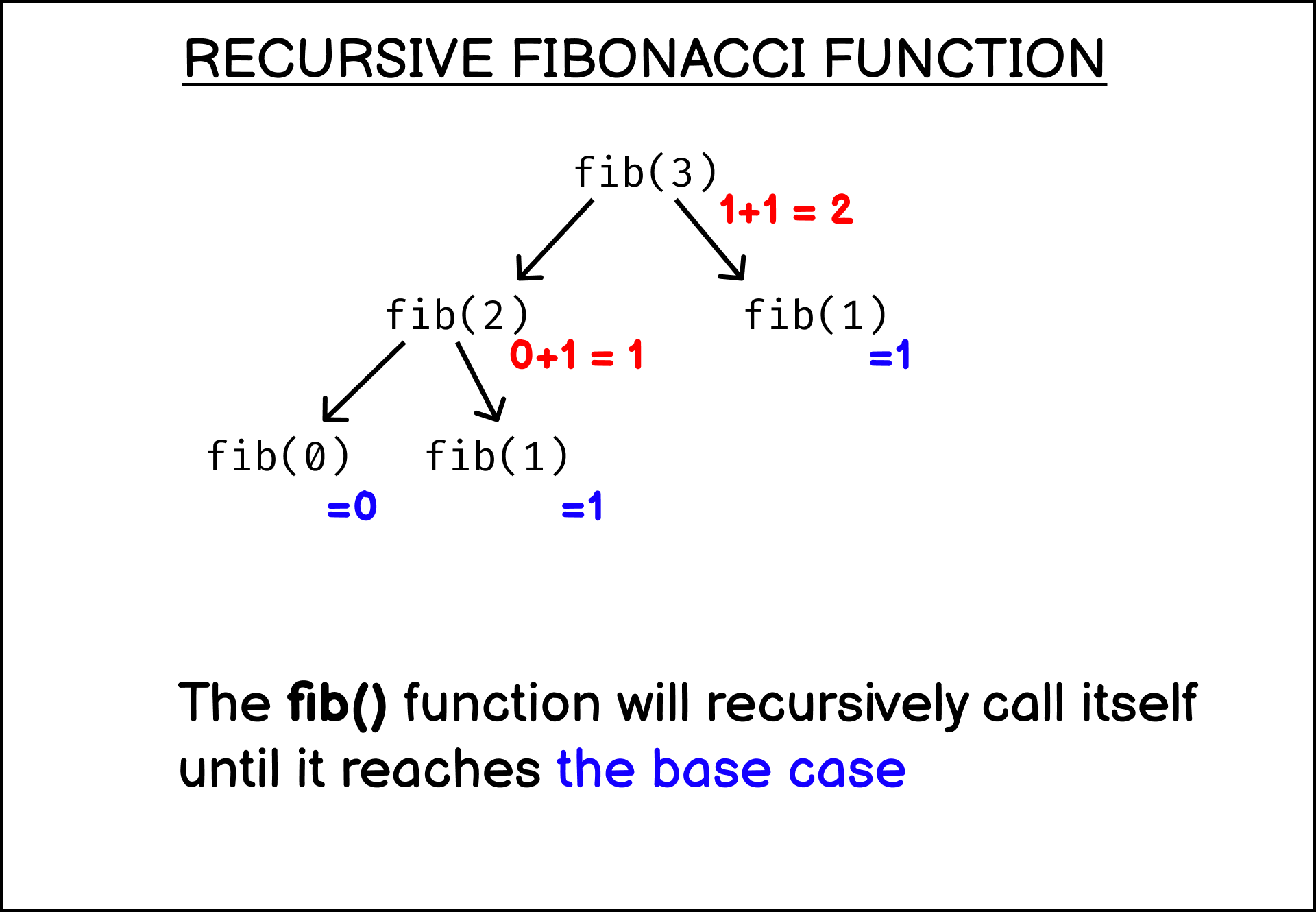
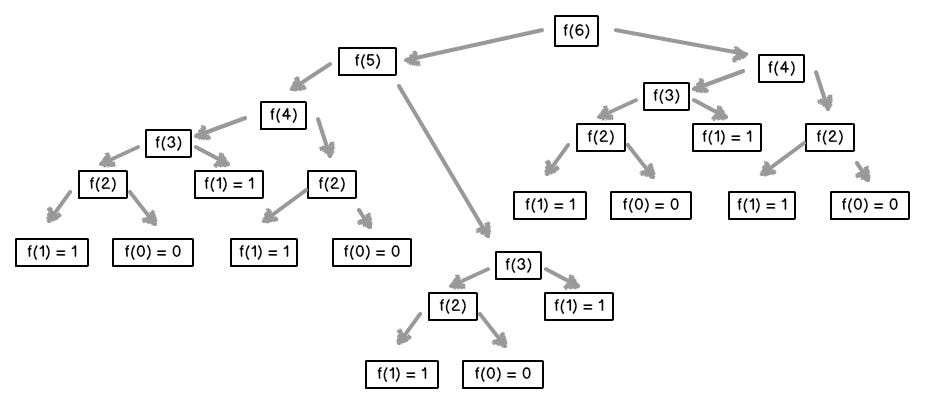



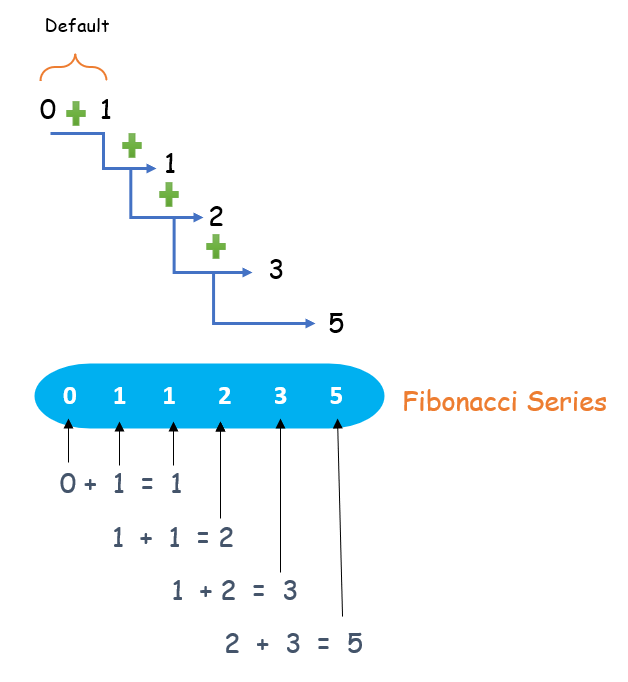


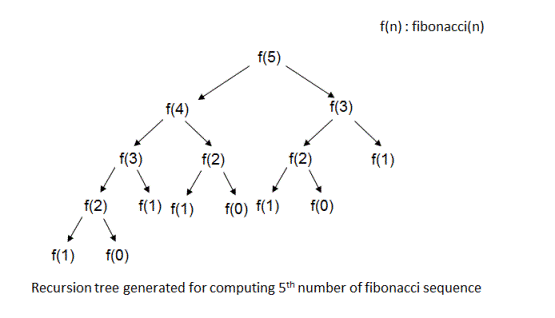
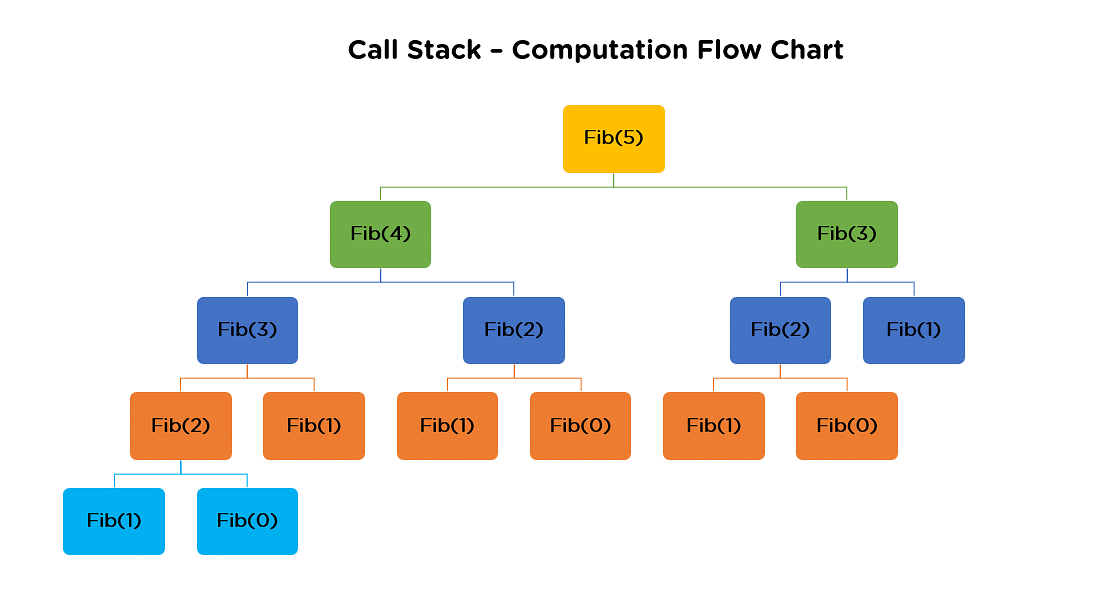



.jpg)


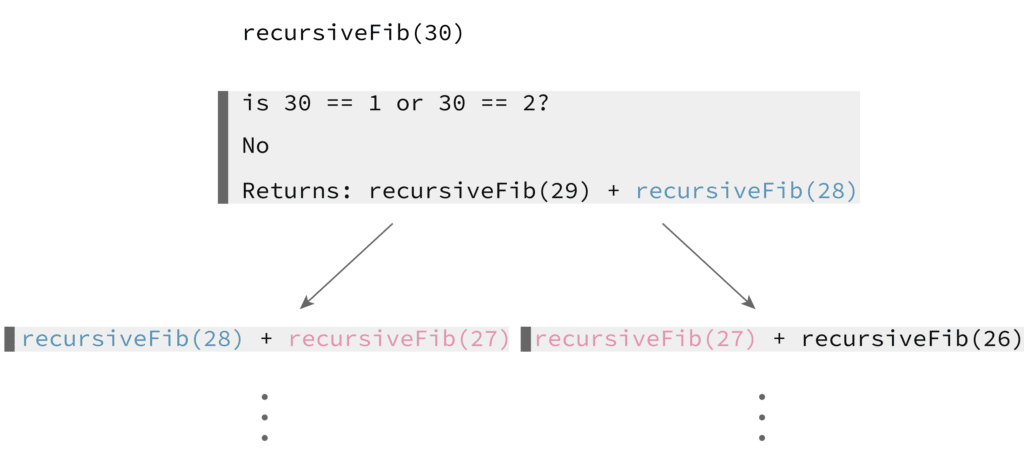





+%3D+1+F(2)+%3D+1.jpg)









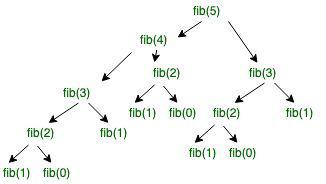
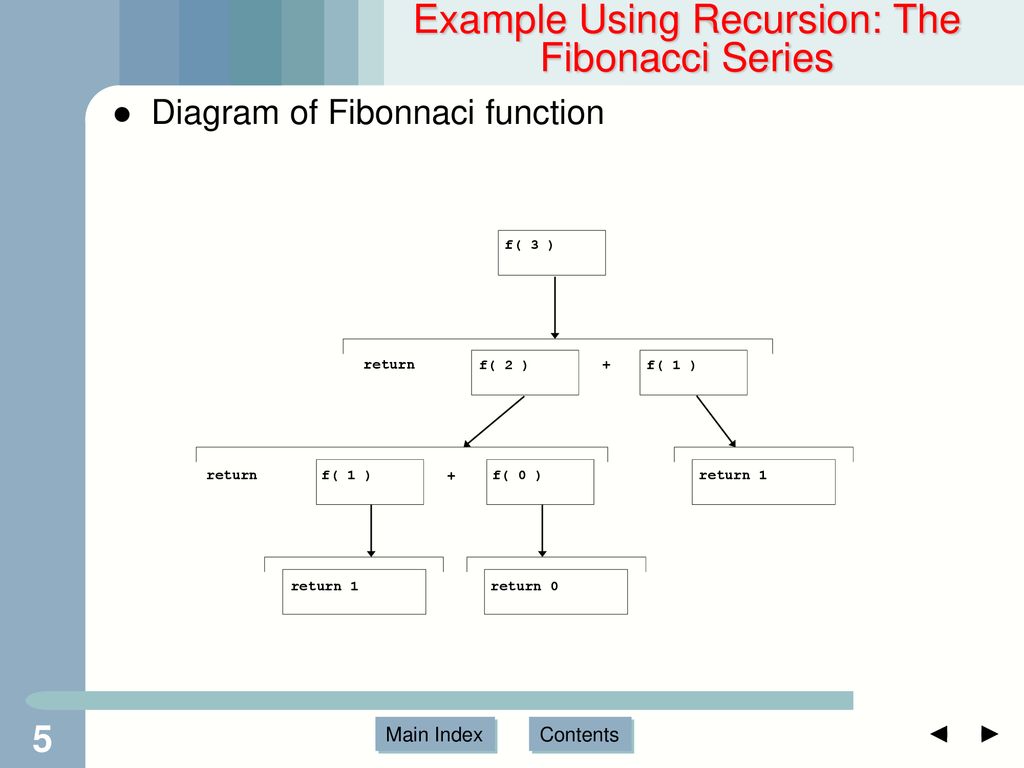
.jpg)

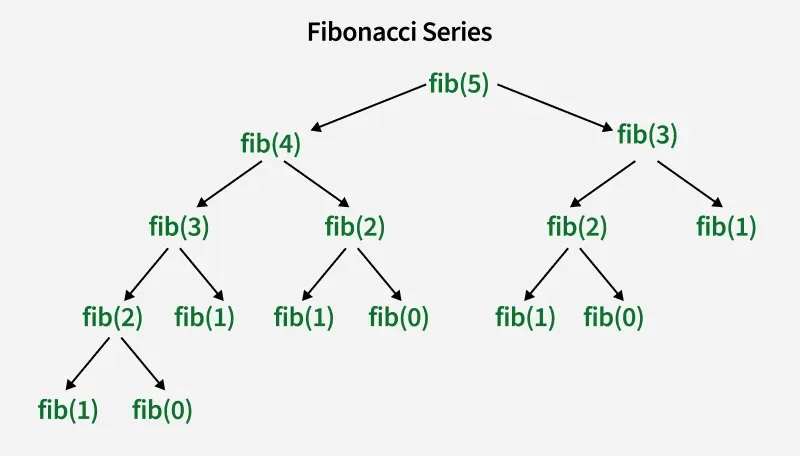













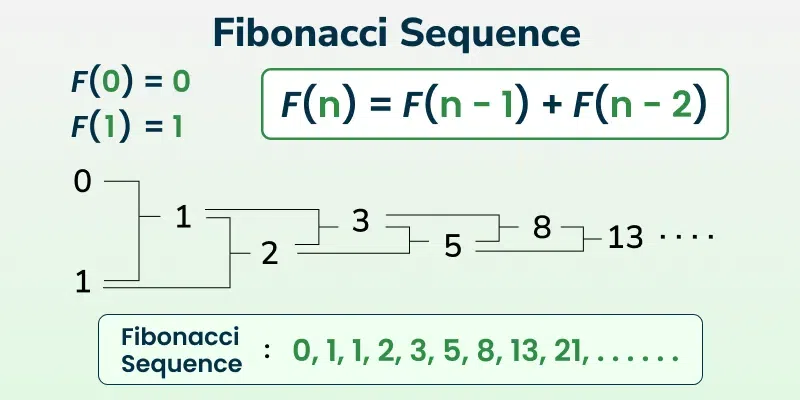
%3D0%2C+F(1)%3D1%2C+F(2)%3D1%2C+F(3)%3D2%2C%E2%80%A6%E2%80%A6..jpg)