Modulus Math Advanced Math Proofs
Browse our specialized Modulus Math Advanced Math Proofs portfolio with extensive collections of expertly curated photographs. enhanced through professional post-processing for maximum visual impact. supporting commercial, educational, and research applications. Browse our premium Modulus Math Advanced Math Proofs gallery featuring professionally curated photographs. Perfect for marketing materials, corporate presentations, advertising campaigns, and professional publications All Modulus Math Advanced Math Proofs images are available in high resolution with professional-grade quality, optimized for both digital and print applications, and include comprehensive metadata for easy organization and usage. Our Modulus Math Advanced Math Proofs collection provides reliable visual resources for business presentations and marketing materials. Multiple resolution options ensure optimal performance across different platforms and applications. Our Modulus Math Advanced Math Proofs database continuously expands with fresh, relevant content from skilled photographers. Instant download capabilities enable immediate access to chosen Modulus Math Advanced Math Proofs images. Regular updates keep the Modulus Math Advanced Math Proofs collection current with contemporary trends and styles. Advanced search capabilities make finding the perfect Modulus Math Advanced Math Proofs image effortless and efficient. Whether for commercial projects or personal use, our Modulus Math Advanced Math Proofs collection delivers consistent excellence. Diverse style options within the Modulus Math Advanced Math Proofs collection suit various aesthetic preferences.



































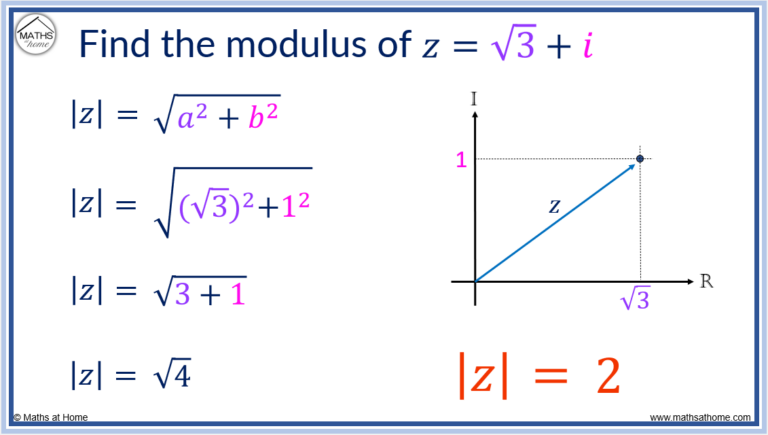






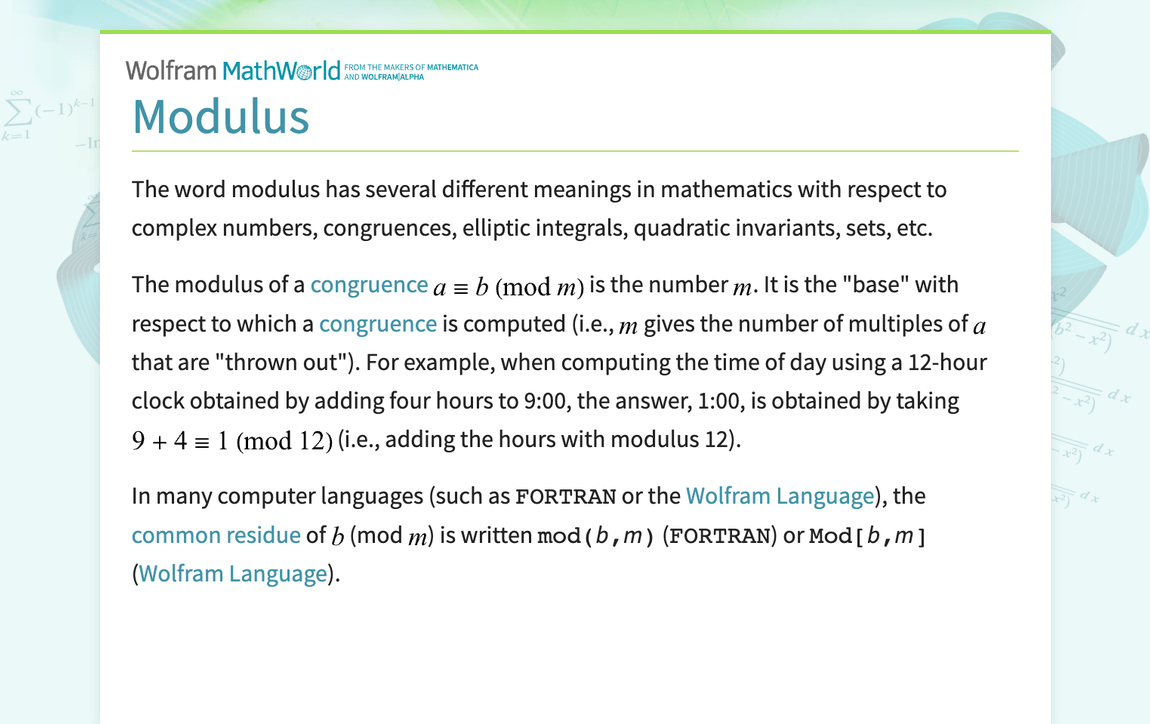


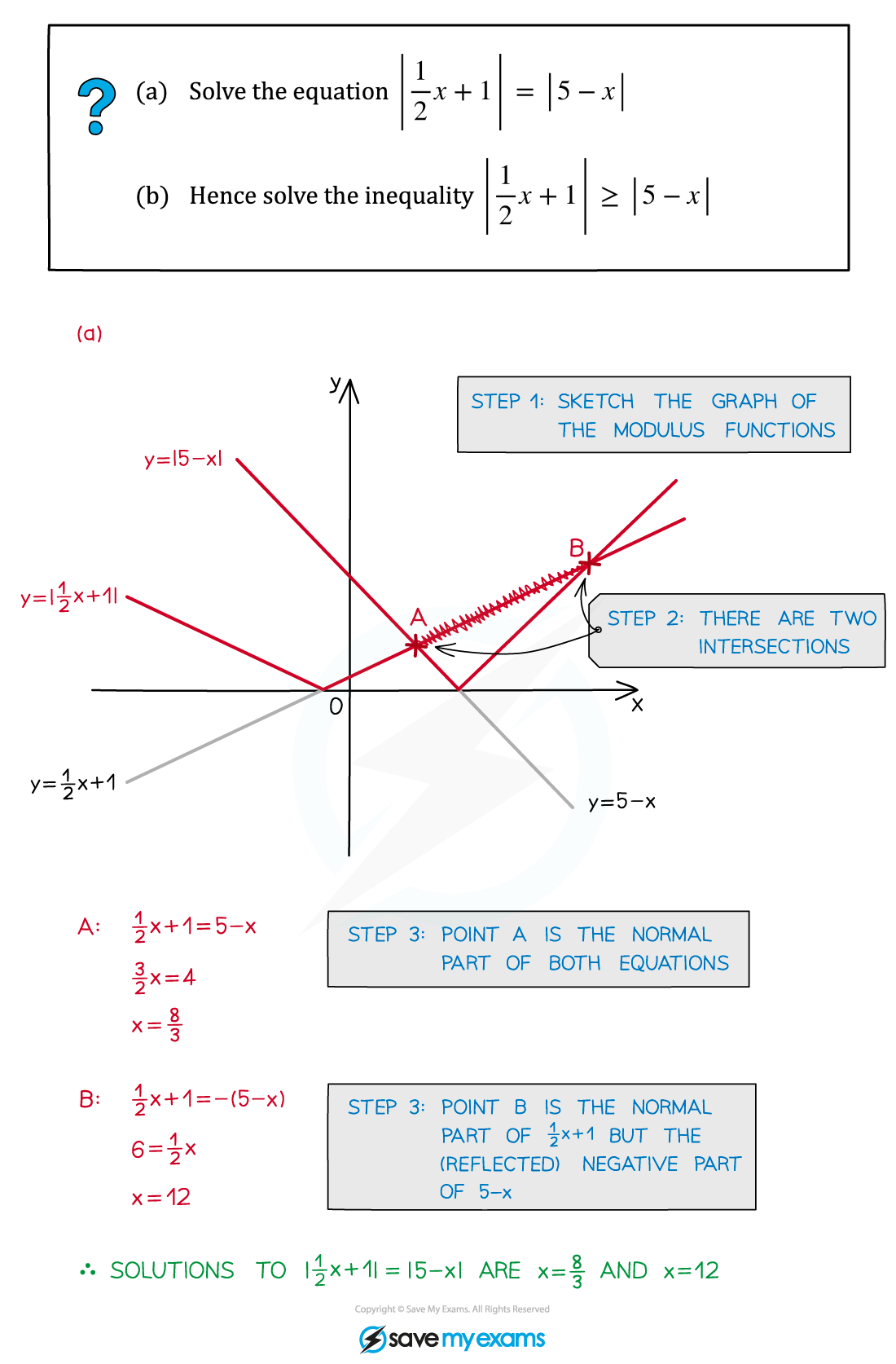












































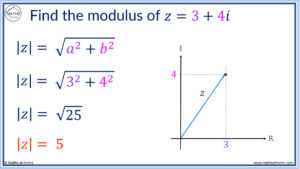



![[Solved] (Properties of Modular Arithmetic). Assume that a, b, c, d and ...](https://mavink.com/images/loadingwhitetransparent.gif)












![[Modular Arithmetic] - The Multiplication Rule Proof and Examples ...](https://i.ytimg.com/vi/c8uxZOFZVeY/maxresdefault.jpg)




+The+remainder+operator+(%25)%2C+known+as+modulus%2C+returns+the+remainder+after+dividing+the+second+operand+into+the+first..jpg)





