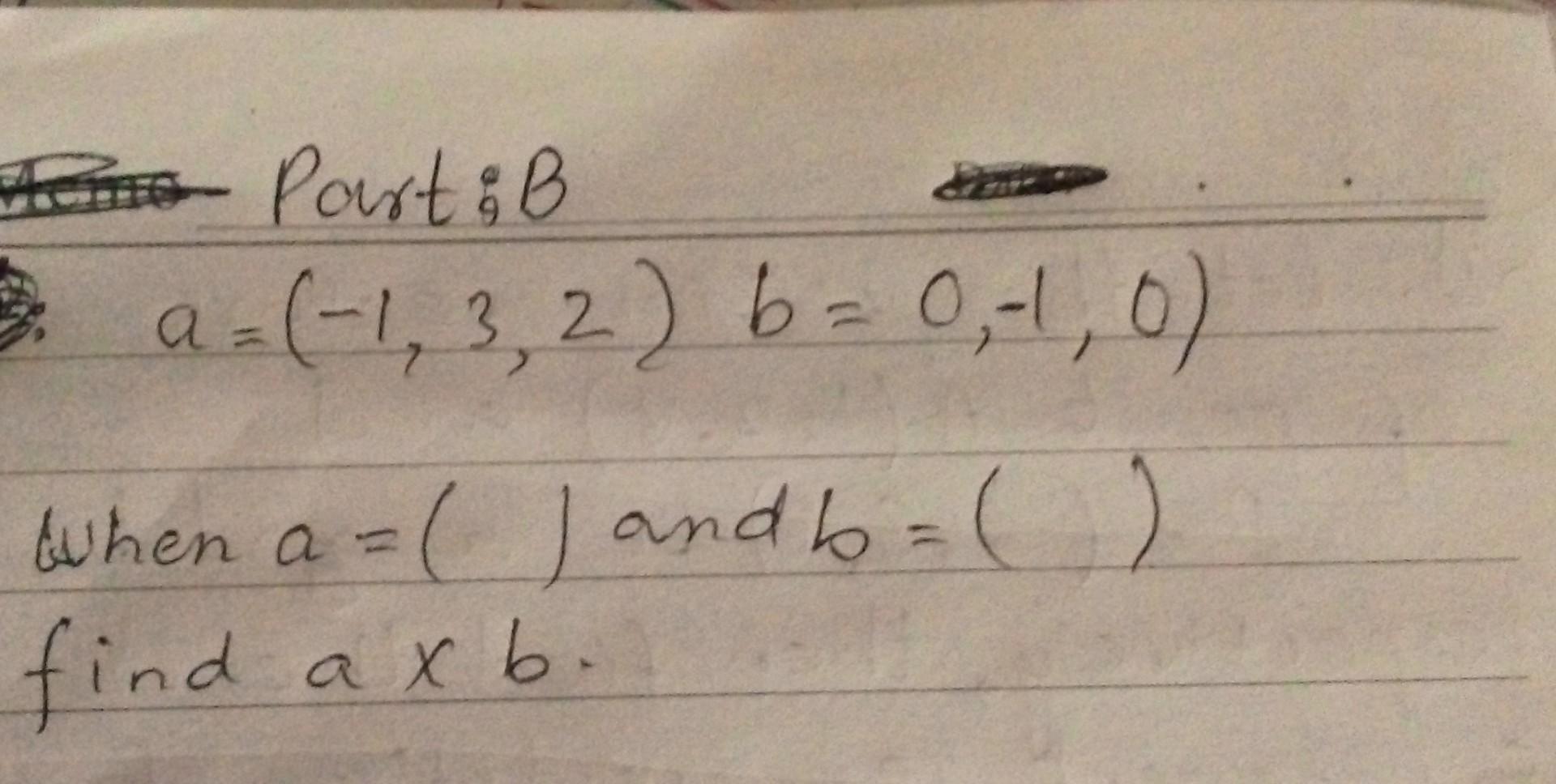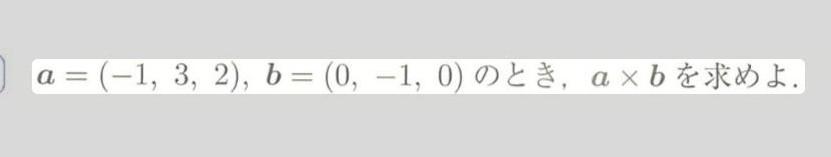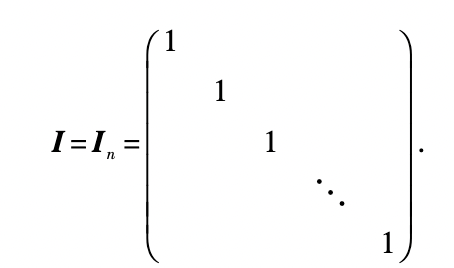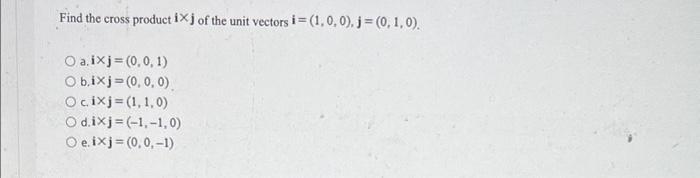Ixj. Matrix
Honor legacy with our historical Ixj. Matrix gallery of extensive collections of timeless images. legacy-honoring highlighting photography, images, and pictures. perfect for historical documentation and education. Discover high-resolution Ixj. Matrix images optimized for various applications. Suitable for various applications including web design, social media, personal projects, and digital content creation All Ixj. Matrix images are available in high resolution with professional-grade quality, optimized for both digital and print applications, and include comprehensive metadata for easy organization and usage. Explore the versatility of our Ixj. Matrix collection for various creative and professional projects. Diverse style options within the Ixj. Matrix collection suit various aesthetic preferences. Multiple resolution options ensure optimal performance across different platforms and applications. Advanced search capabilities make finding the perfect Ixj. Matrix image effortless and efficient. Professional licensing options accommodate both commercial and educational usage requirements. The Ixj. Matrix archive serves professionals, educators, and creatives across diverse industries. Each image in our Ixj. Matrix gallery undergoes rigorous quality assessment before inclusion. Cost-effective licensing makes professional Ixj. Matrix photography accessible to all budgets. Reliable customer support ensures smooth experience throughout the Ixj. Matrix selection process. Instant download capabilities enable immediate access to chosen Ixj. Matrix images. Time-saving browsing features help users locate ideal Ixj. Matrix images quickly.
































![Let A=[a_(ij)] be a square matrix of order 3 such that a_(ij)=2^(j-i ...](https://i.ytimg.com/vi/FY8fLFCsmeg/maxresdefault.jpg?sqp=-oaymwEmCIAKENAF8quKqQMa8AEB-AH-CYAC0AWKAgwIABABGFcgVyhlMA8=&rs=AOn4CLDaNU_6-jcXA1jHbHvw_k96rNdXVw)



 and a(ij)=(3i-2j)^(2), then find matrix A.](https://static.doubtnut.com/ss/web/3594364.webp)













![Solved [Lecture 27] We say that an n xn matrix A = (aij) is | Chegg.com](https://media.cheggcdn.com/media/374/374f8858-a764-40f2-8286-5ed8f0e947ee/php7BvSgr.png)
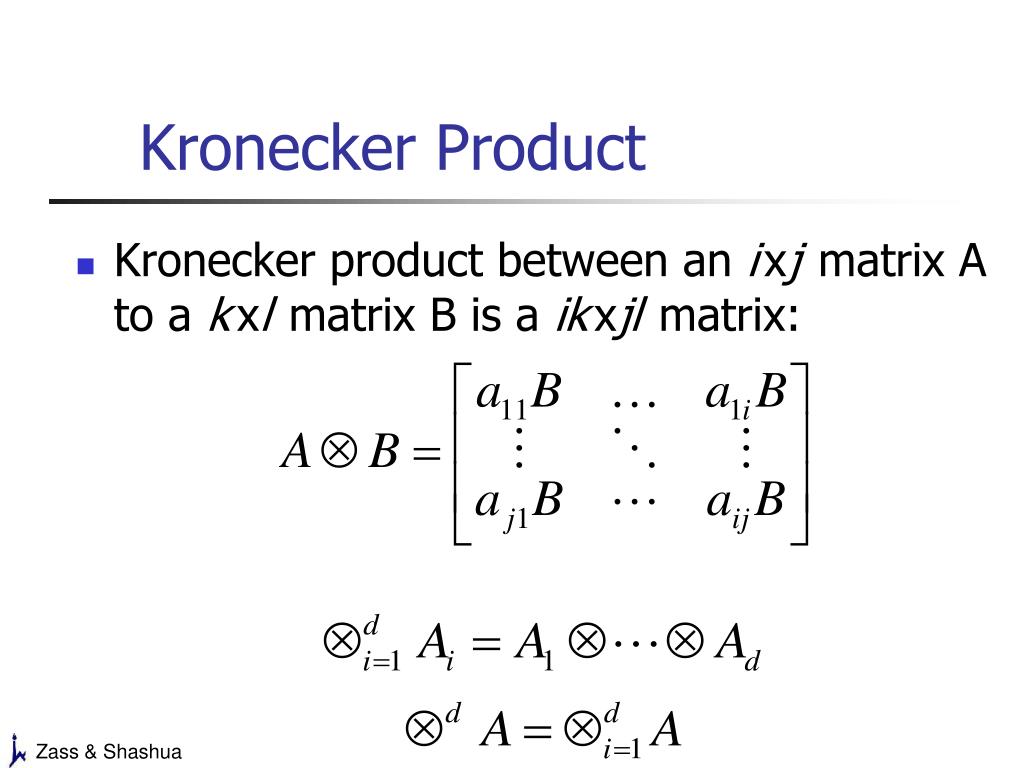





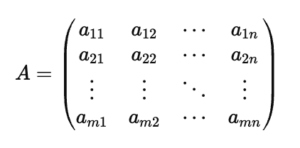

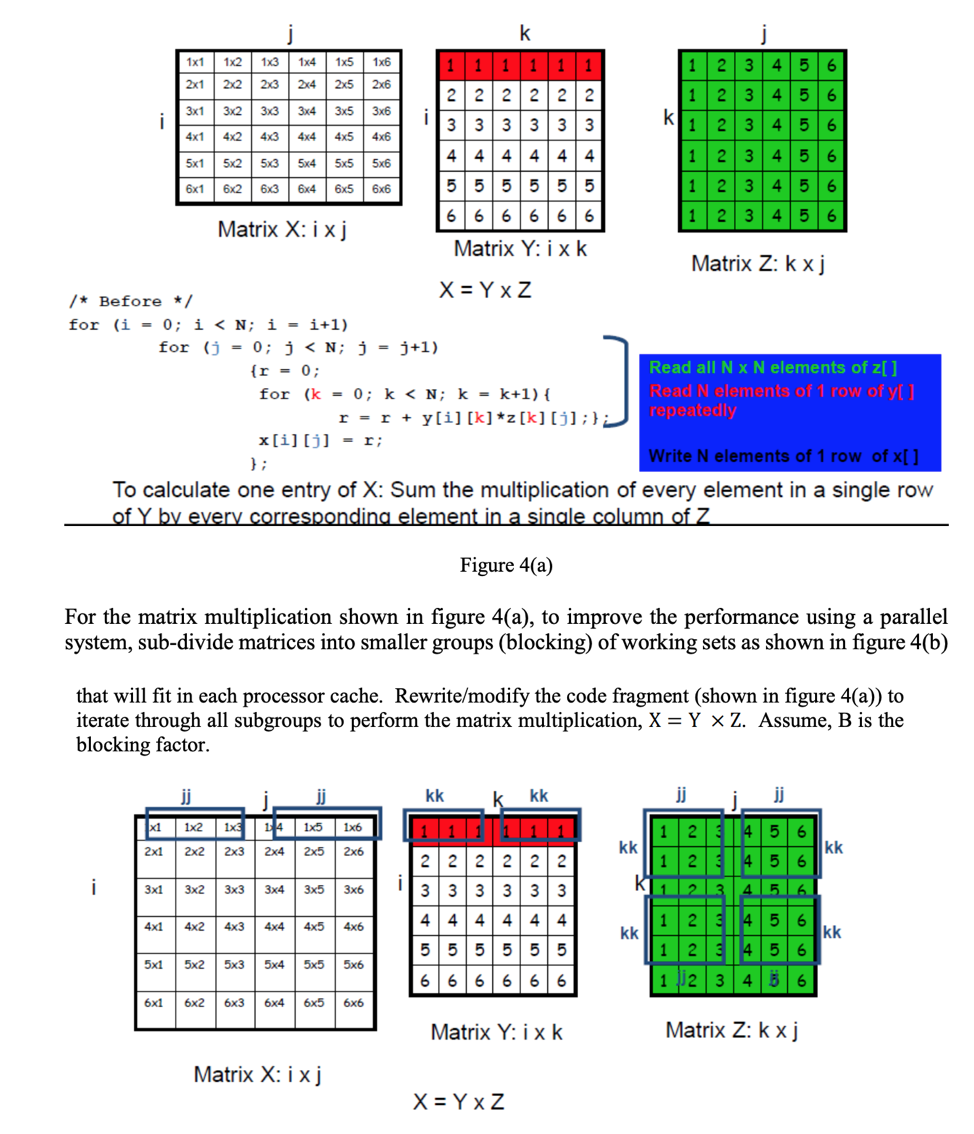













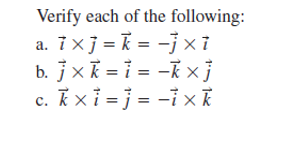

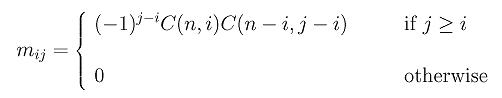
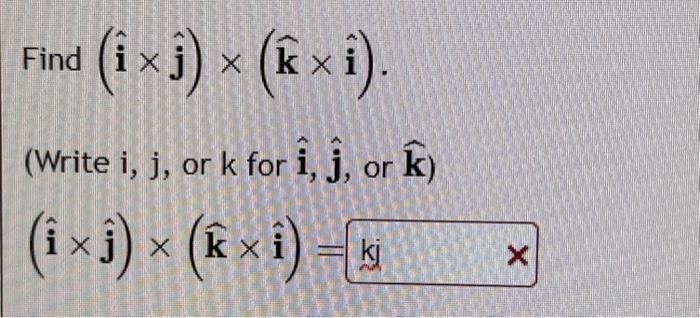
![Solved Problem 3 Given x = [4 1 6] and y = [6 2 7), compute | Chegg.com](https://media.cheggcdn.com/study/ae7/ae7fb845-918d-4df0-b935-c59b0f3c57c2/image)

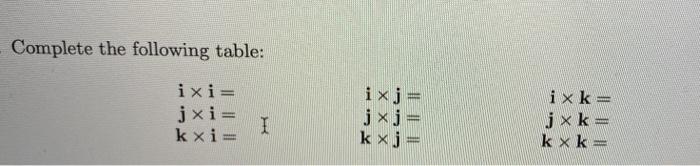


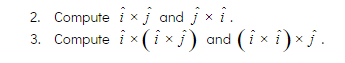





![Solved Problem 3 Given x = [416] and y = [827]. compute the | Chegg.com](https://media.cheggcdn.com/media/57c/57c2c8ad-7637-4b00-a8f0-708ac7262b62/phpj2yOjF)
![Solved Problem 3 Given x = [4 1 6] and y = [6 2 7), compute | Chegg.com](https://media.cheggcdn.com/study/145/145ad4c7-471a-4360-a7a6-f36623bfaf84/image)